Una ecuación exponencial es aquella ecuación en la que la incógnita aparece en el exponente.
Para
resolver una ecuación exponencial debemos tener en cuenta que:
a > 0, a ≠ 1
(a debe ser mayor que cero y distinto de 1)
y que si
(Si la base a es igual a la base a, entonces
los exponentes serán iguales entre sí)
También debemos recordar las propiedades
de las potencias, las que se describen a continuación:
a 0 = 1
Toda potencia elevada a cero es igual a 1
a 1 = a
Toda potencia elevada a 1 es igual a la base
Toda potencia con exponente negativo es igual
al inverso de su base, ahora con exponente positivo en el denominador.
Toda potencia elevada a un exponente fraccionario es igual a una
raíz de la base elevada al numerador de la fracción, y el índice de la
raíz corresponde al denominador de la fracción.
a m • a n = a m+n
Para multiplicar dos potencias de igual base y distintos exponentes,
se conserva la base y esta se eleva a la suma de los exponentes.
a m : a n = a m
− n
Para dividir dos potencias de igual base y distintos exponentes, se
conserva la base y esta se eleva a la resta de dichos exponentes.
(a m) n = a m
· n
Para elevar una potencia a potencia, se
conserva la base y se multiplican los exponentes.
a n • b n = (a
· b) n
Para multiplicar potencias de distinta base, pero
con igual exponente, se multiplican las bases y se conserva el exponente
único o común.
a n : b n = (a
: b) n
Para dividir potencias de distinta base, pero con
igual exponente, se dividen las bases y se conserva el exponente único o
común.
Nota importante
Debemos tener presente que no existe ninguna fórmula general que indique
cómo resolver cualquier ecuación exponencial. Sólo la práctica ayuda a decidir,
en cada caso, qué camino tomar.
De todos modos, para resolver una ecuación exponencial hay que realizar
algunas acciones previas que son imprescindibles:
Primero:
Si los dos miembros de la igualdad tienen distinta
base, debemos reducirlos a la misma base.
Ejemplo 1:
Una vez que tenemos la misma base en los dos miembros,
igualamos los exponentes y resolvemos la ecuación.
Y aquí es donde empiezan las dificultades, ya que si no dominamos las
propiedades de las potencias se hará muy difícil resolver este tipo de
ecuaciones.
Cuando ninguno de los dos lados de la ecuación exponencial puede escribirse como una potencia de la misma base, con frecuencia empezamos tomando logaritmos de ambos lados de la ecuación como en el ejemplo 2.
® log10 = 1
Ejemplo 3
Resuelva la ecuación 5n = 28
Solución Tome logaritmos de ambos lados de la ecuación y despeje n
Solución Tome logaritmos de ambos lados de la ecuación y despeje n
log 5n = log 28
n log 5 = log 28
n = log 28 / log 5
n = 1,4472 / 0,6990 » 2,0704
TAREA1
Resuelva los 10 primeros ejercicios, acceda a la pagina ecuaciones exponenciales
Las ecuaciones logarítmicas son aquellas en las que aparece la incógnita
o incógnitas dentro de un logaritmo. Por ejemplo: log(x+6)
= 1 + log(x-3)
"Puede ser conveniente repasar el tema: Función logarítmica, antes de continuar"
El
logaritmo que suele aparecer en las ecuaciones logarítmicas es el decimal o el neperiano y, normalmente, siempre la misma base en toda
la ecuación.
Para resolver ecuaciones logarítmicas vamos a tener en cuenta:las propiedades de los logaritmos
Además tenemos que comprobar las soluciones para verificar que no tenemos logaritmos nulos o negativos.
Algunas ecuaciones logarítmicas suelen resolverse expresándolas en forma exponencial. Pero recuerde; es necesario comprobar las ecuaciones logarítmicas para ver si tienen soluciones extrañas. Si al verificar una solución se obtiene el logaritmo de un numero no positivo, significa que esta es extraña.
Resuelve las ecuaciones logarítmicas ecuaciones logarítmicas

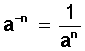









Buena explicación.
ResponderEliminarEcuaciones exponenciales explicadas.
...viaje interestelar aceleración constante (órbitas elípticas)... e, excentricidad >0 y <1 su grado de alargamiento; e=cos B/cos a... elípse, si se define como curva cerrada de la intersección de un plano que corta a una superficie cónica sin pasar por su vértice; a, ángulo de la superficie cónica entre su eje y generatriz; B, ángulo >a y <90º entre el plano y el eje de la superficie cónica.
ResponderEliminar...viaje interestelar aceleración constante (curvas cónicas)... excentricidad, e=cos B/cos a... Circunferencia, curva cerrada: B=90º; como B=90º, el cos B=0, entonces e = 0... Elípse, curva cerrada: B menor de 90º; a menor que B, entonces cos a es mayor que cos B, entonces e > 0 y menor que 1... Parábola, curva abierta: B=a, entonces e = 1... Hipérbola, curva abierta: B menor que a, entonces cos B es mayor que cos a, entonces e > 1... Cónica, si se define como curva de la intersección de un plano que corta a una superficie cónica sin pasar por su vértice; a, ángulo de la superficie cónica entre su eje y generatriz; B, ángulo entre el plano y el eje de la superficie cónica... Si B>a, curva cerrada: el plano corta todas las generatrices.
ResponderEliminar