Dibujo Técnico: Bloques de estudio

Introducción al Dibujo Técnico

BLOQUE 6

La elipse y la Hipérbola 

Informes:
elementos de la elipse dada su ecuación parte 1
elementos de la elipse dada su ecuación parte 2
Ejercicios 
1. Los focos de una elipse son los puntos (-4, -2) y (-4, -6), y la longitud de cada lado recto es 6. hállese la ecuaicon de la elipse y su excentricidad.
2. Los focos de una elipse son los puntos (3, 8) y (3,2) y la longitud de su eje menor es 8. Hallar la ecuación de la elipse, las coordenadas de sus vértices y su excentricidad.
LA HIPÉRBOLA
Una hipérbola es el lugar geométrico de un punto que se mueve en un plano de tal manera que el valor absoluto de la diferencia de sus distancias a dos puntos fijos del plano, llamados focos, es siempre constante.

Elementos de la hipérbola:

 Focos: Son los puntos fijos F y F'.

Centro: Es el punto de intersección de los ejes.

Vértices: Los puntos A y A' son los puntos de intersección de la hipérbola con el eje focal.  Los puntos B y B' se obtienen como intersección del eje imaginario con la circunferencia que tiene por centro uno de los vértices y de radio c.

Radios vectores: Son los segmentos que van desde un punto de la hipérbola a los focos: PF y PF'.

Distancia focal: Es el segmento FF' de longitud 2c.

Eje mayor: Es el segmento AA' de longitud 2a.

Eje menor: Es el segmento BB' de longitud 2b.

 Asíntotas: Son las rectas de ecuaciones: y = -b x ; y = b x

                                                                          a             a

Relación entre los semiejes:  c² = a² + c²
Primera ecuación ordinaria de la hipérbola. Consideremos la hipérbola de centro en el origen y cuyo eje focal coincide con el eje X, y focos los puntos (c, 0) y (- c, 0) es
x² - y² = 1
a²    b²
Si el eje focal coincide con el eje Y , de manera que las coordenadas de los focos  sean (0, c) y  (0,-c), entonces la ecuación es
y² -  x² = 1
a²    b²
Informe:
gráfica de la hipérbola dada su ecuación parte 1 y 2
BLOQUE 5
Objetivo.- Aplicar las ecuaciones de la recta y de las cónicas en la resolución de problemas de la geometría analítica.

contenidos:

Ecuación de la recta que pasa por un punto y tiene una pendiente dada.

Ecuación de la recta dada su pendiente y su ordenada en el origen.

Ecuación simétrica de la recta.

Forma general de la ecuación de una recta.

Informes, ver vídeos
1. encontrar la ecuación de la recta
2. encontrar el punto p dado la pendiente
Ecuación de la circunferencia
Definición.- circunferencia es el lugar geométrico que se mueve en un plano de tal manera que se se conserva siempre a una distancia constante de un punto fijo de ese plano.

Informes, ver vídeos
1. ecuación de la circunferencia
2. ecuación de la circunferencia y es tangente a una recta


LA PARÁBOLA
Definición.- una parábola es el lugar geométrico de un punto que se mueve en un plano de tal manera que su distancia de una recta fija, situada en el plano, es siempre igual a su distancia de un punto fijo del plano y que no pertenece a la recta.

Teorema 1. La ecuación de una parábola de vértice en el origen y eje el eje X, es y² = 4px, en donde el foco es el punto (p, 0) y la ecuación de la directriz es x = -p. Si p > 0, la parábola se abre hacia la derecha; si p < 0, la parábola se abre hacia la izquierda.

Si el eje de una parábola coincide con el eje Y, y el vértice esta en el origen, su ecuación es 
x² = 4py
Teorema 2: La ecuación de una parábola de vértice (h, k) y eje paralelo al eje X, es de la forma

(y - k)² = 4p(x - h), siendo p la longitud del segmento del eje comprendido entre el foco y el vértice.

Si p > 0 la parábola se abre hacia la derecha; si p < 0, la parábola se abre hacia la izquierda

Si el vértice es el punto (h, k) y el eje de la parábola es paralelo al eje Y, su ecuación es de la forma 

(x- h)² = 4p(y - k) Si p > 0, la parábola se abre hacia arriba; si p < 0, la parábola se abre hacia abajo. 

Teorema 3: Una ecuación de segundo grado en las variables x y y que carezca del término en xy puede escribirse en la forma

Ax² + Cy² +Dx + Ey + F =0

Informes, ver vídeos

1. hallar la ecuación de la parábola dado su vértice y foco

2. dada la ecuación general de la parábola hallar su gráfica

3. hallar la ecuación de la parábola dado su foco y directriz
BLOQUE 4

Destreza: Conceptualizar las diferentes curvas geométricas a través de sus características y elementos.

Objetivo:  Construir óvalos, ovoides, elipses, parábolas e hipérbolas mediante la aplicación de procedimientos  y técnicas de trazado para ofrecer un resultado gráfico satisfactorio.
1. Curvas geométricas

1.2. Curvas técnicas

Las curvas técnicas tienen muchas aplicaciones en la resolución de problemas de dibujo técnico, ya sean éstos provenientes del ámbito del diseño industrial, arquitectónico o gráfico.

Las curvas de este tipo se configuran mediante la unión de arcos de circunferencia que son tangentes entre sí, dando lugar a la formación de figuras planas que pueden ser cerradas: óvalo, ovoide; o abiertas: espirales, evolvente del círculo, etcétera.

1.3. Curvas cónicas

Las curvas cónicas se obtienen al seccionar un cono de revolución con un plano secante.

Un cono de revolución es un cuerpo geométrico que puede considerarse engendrado por una línea recta denominada generatriz, que se mueve fija en un punto alrededor de un eje y con una dirección circular denominada directriz.

Dependiendo de la inclinación del plano respecto al eje podemos obtener las siguientes cuatro formas:

Si consideramos el eje vertical, obtenemos:

Circunferencia.- Se obtiene al cortar el cono por un plano horizontal.

Elipse.- Se obtiene al cortar el cono por un plano oblicuo, de inclinación menor que la generatriz
Parábola.- Se obtiene al cortar el cono por un plano paralelo a la generatriz

Hipérbola.- Se obtiene al cortar el cono por un plano oblicuo de mayor inclinación que la generatriz. Esta curva tiene dos ramas.

La elipse

Es una curva cerrada y plana formada por puntos que tienen la propiedad de que la suma de las distancias de cada uno de ellos a otros dos fijos, llamados focos, es constante e igual al eje mayor de la elipse. En todos los puntos de la elipse (por ejemplo el Q2) se cumple:

r + r’ = AB

La hipérbola
Es una curva abierta y plana formada por puntos, cuya diferencia de distancias a dos puntos fijos de un plano, llamados focos, es constante. Por tanto se cumple que r – r’ = VV’ Asíntotas Son las rectas tangentes a la curva en el infinito.

La parábola

Es una curva plana, formada por puntos que tienen la propiedad de estar cada uno de ellos equidistante de un punto fijo, llamado foco, y de una recta llamada directriz. En todos los puntos de la curva, por ejemplo el punto F’, se cumple que r = r’ El vértice V es el punto medio de OF, distancia existente entre el foco y la directriz.

Trazo de una hipérbola conociendo vértices y focos
ver vídeo trazo de una hipébola
Trazo de una parábola mediante haces de proyección 
ver vídeo trazo de una parábola
construcción de una elipse con compás conociendo su eje mayor AB = 10 cm
 ver vídeo trazo de una elipse por el método de localización de puntos  
construir una elipse dados los dos ejes AB = 10 cm y CD = 6 cm

ver vídeo trazo de una elipse por el método de proyección de puntos 

BLOQUE 3

Destreza: Construir polígonos, circunferencias y arcos siguiendo instrucciones.

Objetivo:  Construir diferentes clases de trapecios, polígonos, circunferencias y arcos mediante la aplicación de procedimientos  y técnicas de trazado para ofrecer un resultado gráfico satisfactorio.

ACTIVIDADES

1. Construcción de trapecios y trapezoides
2. Construcción de polígonos regulares y estrellados rectos y curvos
3. Trazado de arcos y circunferencias.
4. Rectificación

3.1.1. Construcción de trapecios y trapezoide.

  

3.1.2 Trazado de un arco de circunferencia que pasa por tres puntos.

Se trata de hacer pasar un arco de circunferencia, o bien una circunferencia completa, por tres puntos (no alineados) que se tienen como datos.

OPERACIONES:
- Se unen los tres puntos, dos a dos, por ejemplo A-B y B-C.
- Se trazan las mediatrices de los segmentos AB y BC.
- El punto O, donde se cortan las dos mediatrices, es el centro del arco solicitado.
- Desde este punto se traza el arco o la circunferencia que deberá pasar por los tres puntos.

construcción geométrica paso a paso http://www.euskalnet.net/ibiguri/ abre este vinculo, haz clic en indice, luego en arcos y rectificaciones y selecciona  arco de circunferencia (3 puntos) 
3.1.3. Hallar el centro de una circunferencia cuando se desconoce el valor del radio 
OPERACIONES:

Trace la circunferencia y dos cuerdas  AB y CD que no sean paralelas. Construya perpendiculares en los puntos medios de cada una de ellas. Prolongue las perpendiculares hasta que se corten en O, O será el centro buscado.

3.1.4 Circunferencia que pase por dos puntos... abrir vínculo 

3.1.5 Rectificar un arco de circunferencia, menor de 90º

Se trata de hacer la rectificación de un arco de circunferencia con un valor menor de 90º.

La rectificación trata de poner, mediante operaciones realizadas con los instrumentos de dibujo, un arco de circunferencia (o una circunferencia completa) sobre una línea recta.

En este caso, el arco de circunferencia es menor de 90º.

Se trata por tanto de determinar la longitud del arco AB y colocarla sobre una línea recta.

3.1.6 Rectificación de un arco de 90º......abrir vínculo 

3.1.7 Rectificación de una circunferencia.

Se trata de determinar la longitud de una circunferencia y colocarla en línea recta.

OPERACIONES:

Sobre una recta cualquiera r se lleva tres veces el diámetro de la circunferencia.

Se divide el diámetro en 7 partes iguales (p.e.: en la última parte).

A continuación de los 3 diámetros, se añade 1/7 parte del diámetro. Se obtiene el punto 4.

Se unen los puntos 0 y 4 y se obtiene la rectificación.
3.1.8 construcción de polígonos

Referencias:
trazado de arcos y circunferencias: https://ibiguri.wordpress.com/temas/circunferencias-y-arcos/arc/ 
Contreras Arias Pablo Fabián. CONSTRUCCIONES GEOMÉTRICAS. Quito Ecuador 

BLOQUE 2

Destrezas:

• Desarrollar habilidades de trazar lineas con instrumentos

• Deducir y construir trazos geométricos como: perpendiculares, paralelas, ángulos, circunferencias, triángulos, aplicando procedimientos. 

Eje integrador: conocer las lineas básicas de la geometría para desarrollar la capacidad de crear y construir con precisión figuras geométricas.

Instrumentos
Son herramientas de precisión que cumplen funciones diversas: sirven como instrumentos para tomar medidas o describir circunferencias, como en el caso del compás.

Entre estos elementos: los lápices, las reglas, los rapidógrafos, portaminas, borradores, escuadras, transportadores, compases, normógrafos, etc.
Ángulo
Es la abertura o separación formada por dos lineas que se cortan o tienen un punto común. Las lineas que forman el ángulo se llaman lados o ramas y el punto en que se encuentran se denomina vértice. 

Tarea de consulta:

1.      Definir líneas perpendiculares, paralelas, secantes y segmento; adjunte gráfica en cada caso.

2.   Definición de ángulo y tipos de ángulos; según su medida, su posición, su suma, ángulos entre paralelas y una recta transversal. ángulos en la circunferencia (inscrito, interior y exterior), y en un polígono regular (central, interior y exterior). Adjunte gráficas.
saber mas...
ejercicios interactivos de tipos de ángulos 
ejercicio interactivo de bisectriz

LAMINA 2 En una lamina reproduzca las imágenes de paralelas y bisectrices  de un angulo recto.

Referencias:
Washington Cabezas R. Dibujo Técnico. Quito

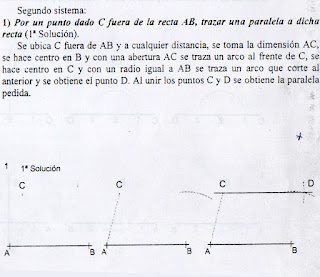
PARALELAS

Se llaman paralelas a dos o más líneas que siguen una misma dirección en todos sus puntos y que por más que se prolonguen no llegan a unirse. Estas pueden ser rectas, curvas mixtas, angulosas u onduladas. 

En el dibujo geométrico tenemos dos sistemas para el trazado de paralelas, el uno con la regla y la escuadra o con dos escuadras y el otro con la regla o escuadra y el compás

LAMINA 3 En una lamina reproduzca las imágenes de paralelas y bisectrices de un ángulo.

DESTREZA

• Reconocer y definir los elementos de la circunferencia para su aplicación en los trazos geométricos.
• Reconocer y construir las clases de triángulos y sus respectivas lineas y puntos notables
• Conocer y construir diferentes clases de polígonos de acuerdo a procedimientos.

Consulta 2.

• Circunferencia: definición y elementos
• Triángulos: definición, clasificación, puntos y lineas notables

saber mas...
ejercicios interactivos de circunferencia ejercicios interactivos de circunferencia
ejercicios interactivos de triángulos ejercicios interactivos de triángulos

FIGURAS PLANAS Y LOS SÓLIDOS

TRIÁNGULOS:

El triángulo es el polígono de menor número de lados, pues está limitado por tres líneas, de ahí, que un triángulo se determina por tres puntos que no están en línea recta.

Clasificación.

Según los ángulos que forman el triángulo, éste se clasifica en:

1)Triángulo rectángulo es el que tiene un ángulo recto, los lados que forman este ángulo se llaman catetos, y el lado opuesto al ángulo recto, hipotenusa.

2)Triángulo acutángulo es el formado por ángulos agudos.

3)Triángulo obtusángulo es el que tiene un ángulo obtuso.

Estos dos últimos triángulos se llaman oblicuángulos porque sus ángulos están constituidos por líneas oblicuas.

Según la igualdad de los lados el triángulo se clasifica en:

4)Triángulo equilátero es el que tiene sus lados y ángulos iguales.

5)Triángulo isósceles es el que tiene sus dos lados iguales.

6)Triángulo escaleno es el triángulo que tiene los tres lados desiguales.

Propiedades de los triángulos.

• La suma de los dos lados de un triángulo es mayor que un tercero.
• En los triángulos equiláteros e isósceles, la altura divide a la base en dos partes iguales
• En todo triángulo, a lados iguales se oponen ángulos iguales.
• Al mayor lado se opone el mayor ángulo.
• La suma de los tres ángulos de un triángulo es igual a 180°

Altura del triángulo es la perpendicular trazada desde el vértice más distante a la base o a su prolongación.

CUADRILÁTEROS.

Cuadrilátero es el polígono que tiene cuatro lados. Hay tres clases de cuadriláteros: el paralelogramo, el trapecio y el trapezoide. La suma de los ángulos interiores de un cuadrilátero es igual a 360°.

1) Paralelogramo es el cuadrilátero que tiene sus lados opuestos iguales y paralelos. El paralelogramo puede ser rectángulo, cuadrado rombo y romboide.

• Rectángulo tiene sus ángulos rectos y sus lados iguales y paralelos de dos en dos.
• Cuadrado tiene los cuatro ángulos rectos y sus cuatro lados iguales y para­lelos
• Rombo es el que tiene los lados iguales y sus ángulos oblicuos iguales de dos en dos.
• Romboide tiene sus lados desiguales y sus ángulos oblicuos iguales de dos en dos, fig.55

2) Trapecio es el cuadrilátero que tiene sólo dos de sus lados paralelos y desiguales, llamadas bases. Hay diferentes clases de trapecios.

• Trapecio isósceles es la figura que tiene iguales los dos lados no paralelos y los dos lados paralelos desiguales.
• Trapecio rectangular es la figura que tiene uno de los lados perpendicular a las bases.
• Trapecio escaleno es la figura que tiene sus lados y ángulos desiguales. 

3) Trapezoide es la figura que tiene sus ángulos desiguales, también sus lados  son desiguales y no paralelos.

CIRCUNFERENCIA.

Circunferencia es una curva formada por puntos, situados en un plano, equidistantes de un punto interno, llamado centro.

Cuerda es el segmento que une dos puntos cualesquiera de la circunferencia.

Arco es una porción de la circunferencia, limitada por dos puntos, llamados extremos del arco.

Diámetro es la cuerda que pasa por el centro del círculo.

Radio es la línea que une el centro del círculo con un punto cualquiera de la circunferencia.

Secante es la recta que corta la circunferencia en dos puntos.

Tangente es la recta que toca la circunferencia en un solo punto.

Sagita es la perpendicular que comienza en el centro de la cuerda y termina en un punto de la circunferencia.

LAMINA 4
Construcción de triángulos y cuadriláteros. segmentos R=5 cm; S=3 cm y T=2 cm

Construir un cuadrado conociendo su lado R=5 cm
Trace AB igual a R, levante una perpendicular en el extremo A. Con la abertura del compás igual a AB, centrando en A, describa el arco que determinará sobre la perpendicular el punto C. Con el mismo radio, centrando respectivamente en C y en B, trace los arcos que se cortaran en D. Uniendo D con C y con B, obtendrá el cuadrado pedido. 

EVALUACIÓN
Conteste falso o verdadero 

El triángulo escaleno tiene sus tres lados iguales ................

El triángulo isósceles tiene los dos lados iguales y uno desigual ..................
El triángulo obtusángulo  tiene un ángulo agudo y dos obtusos ..................

El triángulo equilátero tiene todos sus lados iguales ................

El triángulo acutángulo tiene un ángulo obtuso y dos agudos ...................
Escoge la opicon corecta, resuelve e imprime ejercicios interactivos de triángulos

límites de funciones

Límites de funciones
Destreza: Calcular, de manera intuitiva, el límite cuando h ® 0  de una función cuadrática con el uso de la calculadora como una distancia entre dos número reales.
Criterio de evaluación: Aplica el álgebra de límites como base para el cálculo diferencial.
Indicadores de evaluación. Emplea el concepto de límites en sucesiones convergentes y sucesiones reales; opera con funciones escalonadas.

Definición de limite.  Un número real L es el límite de una función ƒ(x) cuando x tiende a x_o  si para cualquier número real positivo ε, existe un número real δ, tal que si 0 < |x - x₀|< δ, entonces |ƒ(x)-L|< ε.

Lo simbolizamos escribiendo:

                 lim ƒ(x) = L

                 x→x₀

A menudo nos interesa conocer el comportamiento de una función cuando la variable independiente se aproxima a un cierto valor. Esta información nos la proporcionara el estudio de los límites de dicha función.

ecuaciones exponencial y logarítmicas

Una ecuación exponencial es aquella ecuación en la que la incógnita aparece en el exponente.

Para resolver una ecuación exponencial debemos tener en cuenta que:

a > 0, a ≠ 1

(a debe ser mayor que cero y distinto de 1)

y que si 

(Si la base a es igual a la base a, entonces los exponentes serán iguales entre sí)

También debemos recordar las propiedades de las potencias, las que se describen a continuación:

a ⁰ = 1

Toda potencia elevada a cero es igual a 1

a ¹ = a

Toda potencia elevada a 1 es igual a la base

Toda potencia con exponente negativo es igual al inverso de su base, ahora con exponente positivo en el denominador.

 

Toda potencia elevada a un exponente fraccionario es igual a una raíz de la base elevada al numerador de la fracción, y el índice de la raíz corresponde al denominador de la fracción. 

a ^m • a ⁿ = a ^m+n

Para multiplicar dos potencias de igual base y distintos exponentes, se conserva la base y esta se eleva a la suma de los exponentes.

a ^m : a ⁿ = a ^{m − n} 

Para dividir dos potencias de igual base y distintos exponentes, se conserva la base y esta se eleva a la resta de dichos exponentes.

(a ^{m) n} = a ^{m · n}

Para elevar una potencia a potencia, se conserva la base y se multiplican los exponentes.

a ⁿ • b ⁿ = (a · b) ⁿ

Para multiplicar potencias de distinta base, pero con igual exponente, se multiplican las bases y se conserva el exponente único o común.

a ⁿ : b ⁿ = (a : b) ⁿ

Para dividir potencias de distinta base, pero con igual exponente, se dividen las bases y se conserva el exponente único o común.

Nota importante

Debemos tener presente que no existe ninguna fórmula general que indique cómo resolver cualquier ecuación exponencial. Sólo la práctica ayuda a decidir, en cada caso, qué camino tomar.

De todos modos, para resolver una ecuación exponencial hay que realizar algunas acciones previas que son imprescindibles:

Primero:

Si los dos miembros de la igualdad tienen distinta base, debemos reducirlos a la misma base.

Ejemplo 1: 

Una vez que tenemos la misma base en los dos miembros, igualamos los exponentes y resolvemos la ecuación.

 

Y aquí es donde empiezan las dificultades, ya que si no dominamos las propiedades de las potencias se hará muy difícil resolver este tipo de ecuaciones. 

Cuando ninguno de los dos lados de la ecuación exponencial puede escribirse como una potencia de la misma base, con frecuencia empezamos tomando logaritmos de ambos lados de la ecuación como en el ejemplo 2.

    

 ® log10 = 1

Ejemplo 3

Resuelva la ecuación 5ⁿ = 28
Solución Tome logaritmos de ambos lados de la ecuación y despeje n

log 5ⁿ  = log 28

n log 5 = log 28

n = log 28 / log 5

          n = 1,4472 / 0,6990 » 2,0704

TAREA1

Resuelva los 10 primeros ejercicios, acceda a la pagina ecuaciones exponenciales 

Las ecuaciones logarítmicas son aquellas en las que aparece la incógnita o incógnitas dentro de un logaritmo. Por ejemplo: log(x+6) = 1 + log(x-3)

"Puede ser conveniente repasar el tema: Función logarítmica, antes de continuar"

El logaritmo que suele aparecer en las ecuaciones logarítmicas es el decimal o el neperiano y, normalmente, siempre la misma base en toda la ecuación.

Para resolver ecuaciones logarítmicas vamos a tener en cuenta:las propiedades de los logaritmos

Además tenemos que comprobar las soluciones para verificar que no tenemos logaritmos nulos o negativos.

Algunas ecuaciones logarítmicas suelen resolverse expresándolas en forma exponencial. Pero recuerde; es necesario comprobar las ecuaciones logarítmicas para ver si tienen soluciones extrañas. Si al verificar una solución se obtiene el logaritmo de un numero no positivo, significa que esta es extraña.

Ejemplo 4

TAREA 2

Resuelve las ecuaciones logarítmicas ecuaciones logarítmicas