¿QUE ESTUDIAREMOS?
DESTREZA:
CN.F.5.1.3.
Obtener la velocidad instantánea empleando el gráfico posición en función del
tiempo, y conceptualizar la aceleración media e instantánea, mediante el
análisis de las gráficas velocidad en función del tiempo.
CN.F.5.1.4.
Elaborar gráficos de velocidad versus tiempo, a partir de los gráficos posición
versus tiempo; y determinar el desplazamiento a partir del gráfico velocidad vs tiempo.
I.CN.F.5.1.2.
Obtiene a base de tablas y gráficos las magnitudes cinemáticas del MRUV como:
posición, velocidad, velocidad media e instantánea, aceleración, aceleración
media e instantánea y desplazamiento. (I..I.2.)
MOVIMIENTO
MOVIMIENTO
CINEMÁTICA.Es la rama de la mecánica que describe el movimiento de los objetos sólidos sin considerar las causas que lo originan (las fuerzas) y se limita, principalmente, al estudio de la trayectoria en función del tiempo. Para ello utiliza velocidades y aceleraciones, que describen cómo cambia la posición en función del tiempo.
DESCRIPCIÓN DEL MOVIMIENTOConversión de unidades de rapidez
El récord oficial de rapidez terrestre es de 1228,03
km/h, establecido por Andy Green el 15 de octubre de 1997 en el auto a reacción
Thrust SSC. Exprese esta rapidez en m/s.
El prefijo k indica
103, por lo que 1228,03 km/h = 1228,0 3 x 103 m/h.
Sabemos también que hay 3600s en 1h, así que debemos combinar la rapidez de
1228,03 x 103 m/h y un factor de 3600s.
El
proceder correcto es incluir las unidades en el factor, el cual acomodaremos a
modo de eliminar la unidad de horas:
1228,03 km = 1228,0 3 x 103 m x 1h = 341,11 m
h h 3600s s
1228,03 km = 1228,0 3 x 103 m x 1h = 341,11 m
h h 3600s s
Hablar de movimiento es hablar de cambio de posición con respecto a un sistema de referencia. Se habla de que todo se mueve, ¿pero se mueve con respecto a qué?, ¿A caso podría existir un sistema de referencia universal inmóvil? Pues no, porque este último se estaría moviendo con respecto a cualquier otro sistema de referencia.
Un Sistema de referencia es un sistema de coordenadas cartesianas, más un reloj, respecto a los cuales describimos el movimiento de los cuerpos.
Trayectoria corresponde al camino seguido por una partícula o un cuerpo que se desplaza.
Trayectoria corresponde al camino seguido por una partícula o un cuerpo que se desplaza.
Magnitudes vectoriales del movimiento.
Posición, Desplazamiento, Velocidad media, Velocidad instantánea, Aceleración media y instantánea.
Posición se puede expresar como un vector por su ubicación con respecto a un sistema de referencia.
Posición, Desplazamiento, Velocidad media, Velocidad instantánea, Aceleración media y instantánea.
Posición se puede expresar como un vector por su ubicación con respecto a un sistema de referencia.
Desplazamiento es un vector que determina el cambio de posición y la distancia desplazada es el módulo del desplazamiento.
La velocidad instantánea es la velocidad que tiene un móvil en un instante de tiempo.
La velocidad instantánea es el límite del desplazamiento dividido por el tiempo transcurrido en el instante t cuando ese lapso de tiempo tiende a cero.
Vemos que el vector de la velocidad instantánea, por las propiedades matemáticas de la derivación, es tangente a la trayectoria en un tiempo t.
También se puede definir como el límite de la velocidad media cuando el lapso de tiempo tiende a cero.
Cálculo de la velocidad instantánea
En Física decimos que un cuerpo tiene aceleración cuando se produce un cambio del vector velocidad, ya sea en módulo o dirección.
Aceleración media.
Imagina que en un momento to un móvil lleva una velocidad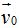 y en el instante
y en el instante 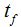 su velocidad es
su velocidad es 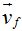 . Llamamos aceleración media al cociente de la variación o cambio de velocidad
. Llamamos aceleración media al cociente de la variación o cambio de velocidad 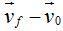 entre el intervalo de tiempo
entre el intervalo de tiempo 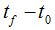 en el que se ha producido dicho cambio:
en el que se ha producido dicho cambio:
Aceleración media.
Imagina que en un momento to un móvil lleva una velocidad
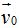 y en el instante
y en el instante 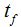 su velocidad es
su velocidad es 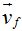 . Llamamos aceleración media al cociente de la variación o cambio de velocidad
. Llamamos aceleración media al cociente de la variación o cambio de velocidad 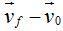 entre el intervalo de tiempo
entre el intervalo de tiempo 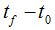 en el que se ha producido dicho cambio:
en el que se ha producido dicho cambio:
Se define la aceleración instantánea, o simplemente aceleración, como el límite de la aceleración media cuando el intervalo de tiempo considerado tiende a 0. También se define de manera equivalente como la derivada de la velocidad respecto al tiempo. Su expresión viene dada por:
Ejercicio 1
Un bateador golpea la pelota a cierta distancia sobre el suelo con una velocidad de 12 m/s a 50º grados sobre la horizontal; la pelota toca el suelo 2 segundos después. ¿Cuales son las componentes de la velocidad de la pelota en el instante de tocar el suelo? ¿a que distancia horizontal llegó la pelota? ¿A que altura sobre el suelo se batió?
Ejercicio 2
Se quiere cruzar un río y la velocidad de la corriente es de 10 m/s y nuestra lancha que desarrolla una velocidad de 15 m/s perpendicular a la corriente. Calcular. a) Cómo se moverá la lancha con respecto a un observador que se encuentra en la orilla?; b) Tiempo que tarda en atravesar el río si tiene una anchura de 200 m; c) Distancia recorrida por la lancha.
Parcial 2
Dinámica del movimiento circular
Dinámica del movimiento circular
Teoría
http://e-ducativa.catedu.es/44700165/aula/archivos/repositorio/3000/3227/html/1_dinmica_del_movimiento_circular.html
Ejercicio 3
Se aplica una fuerza horizontal de 26 N a una piedra de 0,80 kg para mantenerla girando uniformemente en un circulo horizontal de 0,50 m de radio. Calcule la magnitud de su velocidad o rapidez.
clic aquí para solución
PARCIAL 3
Movimiento circular uniforme
El movimiento circular uniforme (m.c.u.) es un movimiento de trayectoria circular en el que la velocidad angular es constante. Esto implica que describe ángulos iguales en tiempos iguales.Algunas de las principales características del movimiento circular uniforme (m.c.u.) son las siguientes:
Un cuerpo realiza un movimiento circular uniformemente acelerado (m.c.u.a.) cuando su trayectoria es una circunferencia y su aceleración angular es constante.
http://e-ducativa.catedu.es/44700165/aula/archivos/repositorio/3000/3227/html/1_dinmica_del_movimiento_circular.html
Ejercicio 3
Se aplica una fuerza horizontal de 26 N a una piedra de 0,80 kg para mantenerla girando uniformemente en un circulo horizontal de 0,50 m de radio. Calcule la magnitud de su velocidad o rapidez.
clic aquí para solución
PARCIAL 3
Movimiento circular uniforme
El movimiento circular uniforme (m.c.u.) es un movimiento de trayectoria circular en el que la velocidad angular es constante. Esto implica que describe ángulos iguales en tiempos iguales.Algunas de las principales características del movimiento circular uniforme (m.c.u.) son las siguientes:
- La velocidad angular es constante (ω = cte)
- El vector velocidad es tangente en cada punto a la trayectoria y su sentido es el del movimiento. Esto implica que el movimiento cuenta con aceleración normal
- Tanto la aceleración angular (α) como la aceleración tangencial (at) son nulas, ya que la rapidez o celeridad (módulo del vector velocidad) es constante
- Existe un periodo (T), que es el tiempo que el cuerpo
emplea en dar una vuelta completa. Esto implica que las características
del movimiento son las mismas cada T segundos. La expresión para el
cálculo del periodo es
T=2π/ω y es sólo válida en el caso de los movimientos circulares uniformes (m.c.u.) - Existe una frecuencia (f), que es el número de vueltas que da el cuerpo en un segundo. Su valor es el inverso del periodo.
Un cuerpo realiza un movimiento circular uniformemente acelerado (m.c.u.a.) cuando su trayectoria es una circunferencia y su aceleración angular es constante.
Podemos describir la posición de un elemento que se mueve según un movimiento circular uniformemente acelerado, en la forma
Algunas de las principales características del movimiento circular uniformemente acelerado (m.c.u.a.) son las siguientes:
- La aceleración angular es constante (α = cte)
- Existe aceleración tangencial at y es constante. Recuerda que
at=α⋅R , siendo R el radio del movimiento - Existe aceleración normal o centrípeta an responsable del cambio de dirección del vector velocidad. Sin embargo, no es constante sino que depende de la velocidad en el punto considerado. Recuerda que
an=v2R=ω2⋅R - La velocidad angular ω aumenta o disminuye de manera uniforme.
mas información, hacer clic → Parte teórica
PARCIAL 3
1. TEMA: MOVIMIENTO Y FUERZA
1.2 LEYES DE NEWTON
Objetivo. Resolver problemas de estática aplicando la primera ley de Newton.
Tercera ley de Newton.-
Las fuerzas de acción y reacción tienen el mismo módulo y dirección, pero sentidos contrarios. Entonces... ¿por qué no se anulan?
Estas fuerzas no se anulan mutuamente ya que se aplican sobre cuerpos distintos
Aplicaciones
Tu día a día está lleno de ejemplos en los que usas el principio de acción y reacción para poder desenvolverte en tu entorno. Aunque en el tema dedicado a aplicaciones de las leyes de Newton estudiaremos muchos de ellos con detenimiento, comenzamos aquí mostrándote algunos: permanecer de pie, andar,correr, nadar, etc.
Solución
Ejercicios para recuperación de examen de física
Resolver los 10 primeros ejercicios. Nota valida para el Parcial 2
Resolver 20 ejercicios hasta el 30. Nota para el Parcial 3
PARCIAL 3
1. TEMA: MOVIMIENTO Y FUERZA
1.2 LEYES DE NEWTON
Objetivo. Resolver problemas de estática aplicando la primera ley de Newton.
Destreza. CN.F.5.1.16
Indagar los resultados de Aristóteles, Galileo y Newton, para comparar sus
experiencias frente a las razones por las que se mueven los objetos y despejar
ideas preconcebidas sobre este fenómeno, con la finalidad de conceptualizar la primera
ley de Newton (ley de la inercia) y determinar por medio de la experimentación que
no se produce aceleración cuando las fuerzas están en equilibrio, por lo que un
objeto continua moviéndose con rapidez constante o permanece en reposo (1 ley
de Newton o principio de inercia de Galileo)
Motivación
Si estamos acostados y tenemos que levantarnos,
¿Qué es lo que se opone a ponernos de pie? ¿Qué entiendes por inercia?
Cuando decimos que un malabarista está en
equilibrio o decimos “no pierdas el equilibrio”, ¿A que nos referimos?
CONSTRUCCIÓN DEL CONOCIMIENTO
La palabra inercia viene del latín inertia que
significa “inacción”, inmovilidad. En física la entendemos como la oposición
que tienen los cuerpos a cambiar su estado de equilibrio.
Equilibrio significa que se encuentra en reposo o
que está en movimiento rectilíneo uniforme.
Recuerda que la primera ley se sintetiza matemáticamente
en ∑F = 0. Eso quiere decir que la sumatoria de fuerzas es igual a 0
Fuerza Normal
Cuando estamos parados en lo alto de un andamio , el andamio nos sostiene o si nos apoyamos en una pared la pared nos sostiene, si apoyamos una escalera en la pared, la pared y el piso ejercen fuerzas sobre la escalera, estas fuerzas son normales porque son perpendiculares a la superficie de contacto, por lo que es una fuerza de contacto. Entonces diríamos que la fuerza normal, es aquella fuerza perpendicular ejercida por la superficie de contacto sobre el cuerpo.
Fuerza de rozamiento
cuando empujamos un mueble muy grande y no se mueve ¿por qué no se mueve?, ¿se deberá a su peso? pues no, porque si colocamos grasa en la superficie podremos hacer con mas facilidad, el peso no ha variado, pero ¿que ha variado?, ¿qué fuerza hace que se resista a moverse?. esa fuerza que se opone al movimiento es la fuerza de rozamiento. La fuerza de rozamiento es una fuerza de contacto y depende de la fuerza que ejerce la superficie, es decir la fuerza normal . entonces podemos afirmar que la fuerza de rozamiento depende de:
- la superficie de contacto
- la fuerza normal
Entonces el máximo valor de la fuerza de rozamiento sera:
- 𝑓 <= 𝞵N
Donde 𝞵 es el coeficiente de rozamiento y dependerá de los materiales de la superficie de contacto y N es la norma.
La fuerza de rozamiento siempre se oponen al movimiento.
Coeficiente de rozamiento estático.
Cuando queremos empujar un cuerpo hacemos un
esfuerzo y logramos moverlo, sentimos que cuando se está moviendo necesitamos
realizar menor fuerza, esto es debido a la inercia, tenemos dos tipos de coeficientes
de rozamiento, estático y cinético; en donde los valores del coeficiente de
rozamiento estático (µe) es mayor al cinético (µc). el µ es adimensional y
depende de las superficies en contacto.
Utilizando la fórmula de Newton, F=ma. (sumatoria de fuerzas sobre el cuerpo es igual a masa por aceleración). En este caso hay dos fuerzas opuestas, el peso en la dirección del plano inclinado Px y el rozamiento Fr.
En ese instante, la fuerza de rozamiento estática es máxima: Fr = μe N
Por lo tanto en la fórmula de Newton las dos fuerzas se igualan: Px - Fr = 0 ; Px = Fr
Observando hasta qué ángulo de inclinación las dos superficies pueden mantenerse estáticas entre sí, podemos calcular el μe coeficiente de rozamiento estático:
Px = mg sen𝚹
N = Py = mgcos𝚹
Fr = μe N
Sustituyendo en : Px = Fr , obtenemos, mg sen 𝚹 = μe mg cos 𝚹 , simplificando:
tg 𝚹 = μe
Tensión
Cuando tenemos un cuerpo colgado de una cuerda o cuando halamos una cuerda tenemos una tensión y esta es siempre contraria a la fuerza que estamos realizando. La tensión es una fuerza de contacto.
Ejercicio 1
ver vídeo https://www.youtube.com/watch?v=6ixpojuaFOE
Segunda ley de Newton.-
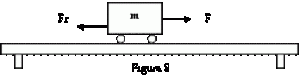
80 N – Fr = 12,5 N
Si despejamos Fr nos queda:
Fr = 80 N – 12,5 N
Fr = 67,5 N
CONTINUACIÓN, PARCIAL 4
Ejercicio a resolver por el estudiante:
Segunda ley de Newton.-
Objetivo: Resolver ejercicios aplicativos a la segunda ley
La Segunda Ley de Newton se encarga de cuantificar el concepto de fuerza. Nos dice que la fuerza neta aplicada sobre un cuerpo es proporcional a la aceleración que adquiere dicho cuerpo. La constante de proporcionalidad es la masa del cuerpo, de manera que podemos expresar la relación de la siguiente manera:
La Segunda Ley de Newton se encarga de cuantificar el concepto de fuerza. Nos dice que la fuerza neta aplicada sobre un cuerpo es proporcional a la aceleración que adquiere dicho cuerpo. La constante de proporcionalidad es la masa del cuerpo, de manera que podemos expresar la relación de la siguiente manera:
F = m a
Esta ley explica qué ocurre si sobre un cuerpo en movimiento actúa una fuerza neta: la fuerza modificará el estado de movimiento, cambiando la velocidad en módulo o dirección.
Ejemplo 1. Un carrito con su carga tiene una masa de 25 Kg. Cuando sobre él actúa, horizontalmente, una fuerza de 80 N adquiere una aceleración de 0,5 m/s2. ¿Qué magnitud tiene la fuerza de rozamiento Fr que se opone al avance del carrito?
Solución
En la figura 8 se muestran las condiciones del problema

La fuerza F, que actúa hacia la derecha, es contrarrestada por la fuerza de roce Fr, que actúa hacia la izquierda. De esta forma se obtiene una resultante F – Fr que es la fuerza que produce el movimiento.
Si aplicamos la segunda ley de Newton se tiene:
Sustituyendo F, m y a por sus valores nos queda
80 N – Fr = 25 Kg. (0,5 m/s²)80 N – Fr = 12,5 N
Si despejamos Fr nos queda:
Fr = 80 N – 12,5 N
Fr = 67,5 N
CONTINUACIÓN, PARCIAL 4
1. Se aplica una fuerza constante de 25 N a un cuerpo de 5 kg de masa inicialmente en reposo. ¿Qué velocidad alcanzará y que espacio habrá recorrido al cabo de 10 segundos? Sol. V = 50 m/s, d = 250 m
2.- ¿Qué fuerza han de ejercer los frenos de un coche de masa 600 kg, que marcha con una velocidad de 54 km/h para detenerlo en 30 m?
3.- Con una fuerza de 200 N se eleva un cuerpo 20 metros en 20 segundos. Calcúlese el peso de dicho cuerpo.
3.- Con una fuerza de 200 N se eleva un cuerpo 20 metros en 20 segundos. Calcúlese el peso de dicho cuerpo.
DATOS:
1. Calcular la masa de un cuerpo que al recibir una fuerza de 20 N adquiere una aceleración de 5 m/s². Sol: 4 kg.
https://www.youtube.com/watch?v=IaPyfc4T1tY
F = 200N
y = 20m
t = 20s
P = ?
y = 20m
t = 20s
P = ?
De la ecuación y = yo + Vot
+ ½ at2, y suponiendo que el cuerpo estaba en reposo y que el sistema
de referencia lo tomamos en yo=0, calculamos a.
20
= 0 + 0 + ½ a (20)2
2(20) =
a
202
a
= 0,1 m/s2
Y
aplicando la 2ª ley Newton:
F
− m·g = m·a
200N
= mg +ma
200N
= m(g+a)
200N =
m
(g + a)
m=
200N/(9,8+ 0,1)m/s2 =20,202 kg
peso P = m·g
P = 20,202 kg·(9,8) m/s2
= 197,97N
4.- Un cuerpo está situado sobre la superficie perfectamente lisa de un plano inclinado de α grados de inclinación. ¿Qué aceleración horizontal debemos comunicar al plano
4.- Un cuerpo está situado sobre la superficie perfectamente lisa de un plano inclinado de α grados de inclinación. ¿Qué aceleración horizontal debemos comunicar al plano
1. Calcular la masa de un cuerpo que al recibir una fuerza de 20 N adquiere una aceleración de 5 m/s². Sol: 4 kg.
2. Calcular la masa de un cuerpo que aumenta su velocidad en 1,8 km/h en cada segundo cuando se le aplica una fuerza de 600N. Sol: 1200 kg.
3. Una fuerza tiene de módulo 4 N y forma un ángulo con el eje positivo x de 30º. Calcula sus componentes. Sol: F = 3,5i + 2j.
4. Dadas las fuerzas F₁ = (3,-8) N y F₂ = (-4,5). Calcula su suma y halla el módulo de la suma. Sol: R = -1i -3j ‖R‖= ⎷10 N
Ver vídeos y presentar informe
Tercera ley de Newton.-
Cuando un cuerpo A ejerce una fuerza
sobre otro cuerpo B, B reaccionará ejerciendo otra
fuerza sobre A de igual módulo y dirección aunque de sentido
contrario. La primera de las fuerzas recibe el nombre de fuerza de acción y la
segunda fuerza de reacción.
FAB→=−FBA→
FAB=FBA
Donde:
FAB→: Es la fuerza de acción de A sobre B y su unidad de medida en el Sistema Internacional (S.I.) es el newton (N)
FBA→: Es la fuerza de reacción de B sobre A y su unidad de medida en el S.I. también es el newton (N)
Algunas observaciones importantes:Las fuerzas de acción y reacción tienen el mismo módulo y dirección, pero sentidos contrarios. Entonces... ¿por qué no se anulan?
Estas fuerzas no se anulan mutuamente ya que se aplican sobre cuerpos distintos
Aplicaciones
Tu día a día está lleno de ejemplos en los que usas el principio de acción y reacción para poder desenvolverte en tu entorno. Aunque en el tema dedicado a aplicaciones de las leyes de Newton estudiaremos muchos de ellos con detenimiento, comenzamos aquí mostrándote algunos: permanecer de pie, andar,correr, nadar, etc.
Ejercicio a resolver
Calcular
la fuerza normal de un cuerpo de 100 kg que se halla sobre un plano inclinado
de 30 metros de base y 15 metros de altura.
diagrama de fuerzas que intervienen
ver vídeo explicativo de la tercera ley https://www.youtube.com/watch?v=VJXNWNEQ75o
impulso y cantidad de movimiento
diagrama de fuerzas que intervienen
ver vídeo explicativo de la tercera ley https://www.youtube.com/watch?v=VJXNWNEQ75o
impulso y cantidad de movimiento
Según el principio de masa, si a ésta se le aplica una fuerza F adquiere
una aceleración a:
F = m·a
Multiplicando ambos miembros por el tiempo t en que se
aplica la fuerza F:
F·t = m·a·t
Como:
a·t =
v
Tenemos:
F·t = m·v
Al término F·t se lo denomina impulso de
la fuerza y al término m·v se lo denomina cantidad
de movimiento.
El impulso de la fuerza aplicada es igual a la cantidad de movimiento que
provoca,
o dicho de otro modo, el incremento de la cantidad de movimiento de
cualquier cuerpo es igual al impulso de la fuerza que se ejerce sobre él
El impulso y la cantidad de movimiento son magnitudes vectoriales.
El impulso y la cantidad de movimiento son magnitudes vectoriales.
Principio de conservación
de la cantidad de movimiento:
Si la resultante de las fuerzas exteriores que actúan
sobre un sistema de partículas es nula, la cantidad de movimiento del sistema
permanece constante.
Ejercicio
Dos bolas de billar, situadas sobre una mesa, impactan
una con la otra. ¿Qué sucede con la cantidad de movimiento de las bolas?
a) La cantidad de movimiento de las dos bolas es la
misma.
b) La cantidad de movimiento del sistema formado por las
dos bolas no varía.
c) La cantidad de movimiento del sistema formado por las
dos bolas aumenta.
d) La cantidad de movimiento del sistema formado por las
dos bolas disminuye.
Solución:
La opción correcta es la b). Las fuerzas que intervienen
en el impacto de las dos bolas son fuerzas interiores. La resultante de las
fuerzas exteriores es nula y la cantidad de movimiento del sistema permanece
constante, según el principio de conservación de la cantidad de
Problema n°
1) Un patinador de
80 kg de masa le aplica a otro de 50 kg de masa una fuerza de 25 kgf durante
0,5 s, ¿qué velocidad de retroceso adquiere el primero y que velocidad final
toma el segundo?
Desarrollo
Datos:
m1 = 80 kg
m2 = 50 kg
1kgf = 9,80665N
Para obtener un resultado aproximado, multiplica el valor de fuerza por 9,807
1kgf = 9,80665N
Para obtener un resultado aproximado, multiplica el valor de fuerza por 9,807
F = 25 kgf = 25 kgf·9,80665 N/1 kgf = 245,17
N
t = 0,5 s
Según la
definición de impulso:
I = F·t
I = 245,17 N·0,5 s
I = 122,58 kg·m/s
El impulso en
el momento del choque es el mismo para ambos cuerpos y el impulso también es
igual a la cantidad de movimiento.
I = m1·v1
I/m1 = v1
v1 = (122,58 kg·m/s)/80 kg
v1 = 1,53 m/s
I = m2·v2
I/m2 = v2
v2 = (122,58 kg·m/s)/50 kg
v2 = 2,45 m/s
Problema n° 1) Una
pelota de béisbol de 0,15 kg de masa se está moviendo con una velocidad de 40
m/s cuando es golpeada por un bate que invierte su dirección adquiriendo una
velocidad de 60 m/s, ¿qué fuerza promedio ejerció el bate sobre la pelota si
estuvo en contacto con ella 5 min?
Problema n° 2) Un hombre colocado sobre patines arroja una
piedra que pesa 80 N mediante una fuerza de 15 N que actúa durante 0,8 s, ¿con
qué velocidad sale la piedra y cuál es la velocidad de retroceso del hombre si
su masa es de 90 kg?
mas
ejercicios
https://www.fisicanet.com.ar/fisica/impulso/tp02_cantidad_de_movimiento.php
descargue este archivo y pase las actividades a su cuaderno de trabajo y resuelva los ejercicios solicitados. clic aquí
descargue este archivo y pase las actividades a su cuaderno de trabajo y resuelva los ejercicios solicitados. clic aquí
1. Un ciclista recorre 5,4 km en 15 min a velocidad constante. Si el diámetro de las ruedas de su bicicleta es de 80 cm, calcula: a) la velocidad angular de las ruedas. b) el número de vueltas que dan las ruedas en ese tiempo.
Sol.: 15 rad/s; b) 2148,59 vueltas
2. La rueda de una bicicleta tiene 30 cm de radio y gira uniformemente a razón de 25 vueltas por minuto. Calcula: a) La velocidad angular, en rad/s. b) La velocidad lineal de un punto de la periferia de la rueda. c) Angulo girado por la rueda en 30 segundos d) número de vueltas en ese tiempo.
Sol.: a) 2,62 rad/s; b) 0,79 m/s; c) 78,6 rad; d) 12,50 vueltas
3. Un avión despega de la pista de un aeropuerto, después de recorrer 1000 m de la misma, con una velocidad de 120 Km/h. Calcular a) la aceleración durante ese trayecto. b) El tiempo que ha tardado en despegar si partió del reposo c) La distancia recorrida en tierra en el último segundo.
Solución: a) a=5/9 m·s-2 b) t=60s; c) s=33,1 m
4. Un coche A que se desplaza a una velocidad de 108 km/h, pasa al lado de otro B que se encuentra en reposo. Dos segundos después de pasar A, arranca B con una aceleración de 5 m/s2 hasta alcanzar una velocidad de 180 km/h. ¿Cuánto tiempo tarda en alcanzarlo y a que distancia del punto de partida?
Test de física para ser bachillerResolver los 10 primeros ejercicios. Nota valida para el Parcial 2
Resolver 20 ejercicios hasta el 30. Nota para el Parcial 3
FÍSICA SUPERIOR
LEYES DE NEWTON-PLANO INCLINADO
CLIC AQUÍ PARA EJERCICIO1 https://www.youtube.com/watch?v=yEVNX3Zj9Mg
PRIMERA LEY DE NEWTON
EJERCICIO2 "Todo cuerpo permanecerá en su estado de reposo o de movimiento rectilíneo uniforme a menos que una fuerza neta externa actúe sobre él"
Ejercicio3. Una partícula de masa m= 0,6 kg, unida a una cuerda de longitud L=80 cm, la cual forma un angulo de 𝛂= 35º con la vertical. Calcular la tensión del cable y la rapidez de la partícula.
EJERCICIO4 movimiento circular, el péndulo cónico . Ecuaciones de la tangente del angulo, velocidad y Periodo. Clic aquí
PARCIAL 3
Momento de una fuerza
Momento de una fuerza
El
torque o momento de fuerza,( representado con la letra griega (tau) τ) es la relación que existe entre la fuerza que
aplicamos y la distancia que hay entre el punto donde se aplica la fuerza y el
eje, esta distancia también es conocida con el nombre de brazo
de palanca.
ejercicio5 clic aquí
PROBLEMA DE EQUILIBRIO TRASLACIONAL Y ROTACIONAL_____________________________________________________________________________
Simulador Ser Bachiller resuelto 2017 resolver las preguntas 2, 3, 14, 17, 22, 26, 28, 32, 38, 39, 40, 97, 105, 107, 216, 217, 218, 219, 220.


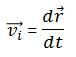






No hay comentarios:
Publicar un comentario