PRUEBA DE DIAGNÓSTICO 🔄hacer cli aquí.
- Magnitudes fundamentales y derivadas
- Magnitudes escalares y vectoriales:
En Física, se llaman magnitudes a aquellas propiedades que pueden medirse y expresar su resultado mediante un número y una unidad. Son magnitudes la longitud, la masa, el volumen, la cantidad de sustancia, el voltaje, etc.
Las siguientes magnitudes se denominan magnitudes físicas fundamentales. Si a estas magnitudes se les añaden dos magnitudes complementarias: el ángulo sólido y el ángulo plano, a partir de ellas pueden expresarse TODAS las demás magnitudes físicas.
De igual forma, es importante definir las magnitudes derivadas más útiles que se exponen en la siguiente tabla:
Indicadores esenciales de evaluación
- Reconoce las unidades del Sistema Internacional.
- Diferencia magnitudes fundamentales y derivadas.
LECCION 1
1. El límite de rapidez en una autopista es de 90 km/h. Si el chofer de un autobús que va conduciendo por ella lo hace a una velocidad equivalente a 28 m/s, ¿está cumpliendo con esta disposición? Explique.
2. Un terreno tiene forma rectangular y mide 18 m de largo por 12 m de ancho. Si el precio del metro cuadrado es $ 15, ¿cuánto cuesta el terreno?
3. Se quieren poner baldosas cuadradas de 25 cm de lado en la pared de un baño que tiene 4,5 m de largo por 2,3 m de altura, ¿cuál es el número de baldosas que se deben colocar?
4. El tanque de combustible de una camioneta se llena con 60 litros, ¿cuántos galones se deben solicitar al expendedor de una gasolinera para llenarlo?, ¿cuál es el costo de hacerlo si cada galón de gasolina súper cuesta $ 2,10?
5. El barril de petróleo es una medida de volumen específica que equivale a 42 galones. ¿Cuál es la cantidad de cm3 contenidos? Si la densidad del petróleo es aproximadamente 0,85 g/cm3, ¿cuántos kg tiene un barril?
MAGNITUDES ESCALARES Y VECTORIALES
- Definir el sentido de ubicación, a partir de la orientación geográfica, polar y rectangular respecto a un sistema de coordenadas.
- Diferenciar magnitudes escalares y vectoriales, a partir de la implementación de procedimientos específicos en su manejo.
formas en las que un vector puede ser representado: rectangular, polar y geográfica.
Algunas magnitudes, no basta con definirlas solo con un
número y una unidad, sino además se debe especificar una dirección y
un sentido que las defina completamente. Estas magnitudes son vectoriales.
Las magnitudes vectoriales son representadas por medio
de vectores.
Por ejemplo, "una velocidad de 30 km/h" queda
totalmente descrita si se define su dirección y sentido: "una velocidad de
30 km/h hacia el norte" a partir de un marco de referencia determinado
(los puntos cardinales).
Entre algunas magnitudes vectoriales comunes en física son:
la velocidad, aceleración, desplazamiento, fuerza, cantidad de movimiento, impulso, peso, campo eléctrico, campo magnético, torque, momentum, entre
otras
Existen diferentes formas de expresar una cantidad vectorial. Una de ellas es la forma polar, que se escribe como un par de coordenadas, en las cuales denotan su magnitud y su dirección. Por ejemplo, La velocidad (30 m/s, 60º), quiere decir "velocidad de 30 m/s a 60º desde el origen del marco de referencia dado".
Las magnitudes escalares se representan únicamente por un número que indica una determinada cantidad. La
masa de un cuerpo, que en el
Sistema Internacional de Unidades se mide en kilogramos, el volumen, que se mide en metros cúbicos, la temperatura o la longitud, son algunos ejemplos de magnitudes escalares.
Ejemplo
La suma de los vectores a y b que aparecen en la figura es igual a:
Opciones de Respuesta: 7u, 3u, 4u, 5u
El vector suma s = a + b; se obtiene, trasladando el vector b al final del vector a y unimos mediante un segmento de recta que va desde el inicio del vector a hasta el final del vector b, formándose un triángulo rectángulo que tiene como componente los vectores a y b.
solución grafica
solución analítica
aplicando el teorema de Pitágoras podemos calcular el módulo del vector suma:
Indicadores esenciales de evaluación
- Ejemplifica y distingue magnitudes vectoriales y escalares
- Encuentra los componentes de un vector
- Calcula el vector resultante a partir de sus componentes
- Establece el vector resultante de la suma o diferencia de varios vectores
- Diseñar una tabla en la que se registre un listado de magnitudes físicas vectoriales y escalares sería beneficioso.
- Se conoce que un barco en mar abierto se desplaza 3,5 km; N 50° E para luego cambiar su rumbo y recorrer 6 km; S 30° E. Determine la posición en la que se encuentra el barco usando tres formas diferentes (método analítico y dos métodos gráficos). Compare las respuestas y determine el porcentaje de error generado en el cálculo tomando al valor obtenido en el método analítico como el valor real.
- Ubicados en el patio de la institución un estudiante verifica que su amigo se encuentra a 15m de distancia en la dirección sur 37° oeste y una pelota se encuentra a 20m en la dirección 323°. Qué distancia y en qué dirección debe caminar el amigo para llegar a la pelota. Si el estudiante quiere llagar a donde su amigo caminando en trayectorias rectas, pero primero pasa por la ubicación de la pelota, cuanto debe recorrer.
POSISICIÓN Y DESPLAZAMIENTO
CN.F.5.1.7. Establecer las diferencias entre vector posición y vector desplazamiento, y analizar gráficas que representen la trayectoria en dos dimensiones de un objeto, observando la ubicación del vector posición y vector desplazamiento para diferentes instantes. CM
Precisiones para la enseñanza y el aprendizaje
Para el estudio del movimiento de los cuerpos (cinemática),
se va a revisar los conceptos que permitirán abordar el tema de movimiento con
respecto a un sistema de referencia por lo que se aclara los conceptos de posición,
trayectoria, distancia y desplazamiento.
Un cuerpo en movimiento deja marcada una huella que se
conoce como trayectoria, y que es el registro del camino recorrido. Será
necesario insistir que la trayectoria no puede ser medida ni calculada, puesto
que no es una magnitud. Según la forma que toma la trayectoria, se acostumbra a
denominar al tipo de movimiento como rectilíneo, circular, parabólico, entre
otros.
Para definir ¿qué es movimiento?, necesitamos en
primer lugar saber que es la posición,
a la que se define como la ubicación en la que se sitúa un objeto con respecto
a un punto referencial. De allí entonces se podría desprender que el movimiento
tiene lugar cuando un cuerpo experimenta cambio de posición. Debe quedar claro
para el estudiante que todo movimiento es relativo dependiendo del sistema de
referencia que se utiliza. Así por ejemplo una persona que está en el interior
de un tren puede considerarse en movimiento con respecto a un observador que se
encuentre en el andén de la estación, pero no está en movimiento con respecto a
otro pasajero sentado en el mismo tren.
La distancia
es la longitud que un objeto se mueve a lo largo de una trayectoria.
El desplazamiento
es el cambio de posición que experimenta un objeto. (El símbolo Δ se utiliza para indicar “cambio de”
o “variación de”). Un gráfico como el que se muestra puede ayudar a aclarar las
dudas.

TIC (tecnologías de la información y la comunicación)
Se puede acceder a la dirección electrónica http://www.educaplus.org/movi/index.html y encontrar varias aplicaciones referentes a conceptos cinemáticos ubicados en la parte derecha de la pantalla: posición de un punto, vector posición, trayectoria, distancia y desplazamiento, que aluden a los temas tratados en este apartado.
La posición es una magnitud vectorial, ya que a más de módulo requiere de una dirección para ser perfectamente entendida. Igual es el caso del desplazamiento, pues de no existir la dirección no se conocería hacia dónde se mueve el objeto. Generalmente al aparecer valores como el de una posición negativa, por ejemplo – 45 km, los estudiantes no comprenden como un valor de posición puede ser negativo, ante lo cual el docente debe recalcar que el signo está indicando la dirección que se haya asignado con ese signo (izquierda u oeste, abajo o sur, afuera, etc.), al igual que el signo positivo indicaría las direcciones contrarias a las mencionadas.
La distancia en cambio es una magnitud escalar, pues solamente interesa cuantificar la longitud del recorrido.
Ejemplo1
Una casa está ubicada en un bloque de viviendas de forma cuadrada de 80 m de lado. Si un morador de dicha casa da una vuelta completa a la manzana, realizaría un recorrido que se observa en la gráfica:
La distancia recorrida como es notoria será igual al valor correspondiente a la suma de los valores de las distancias laterales recorridas, y así sabemos que son 320 m de distancia recorrida. No obstante, podemos notar que el desplazamiento es cero, debido a que la posición inicial y final del objeto coinciden.
La única forma posible de conseguir que la magnitud del desplazamiento coincida con el valor de la distancia recorrida, es que la trayectoria seguida por el cuerpo en movimiento sea una línea recta dirigida en un solo sentido.
Ejemplo2
1. Un
hombre se encuentra inicialmente en el punto P. Se mueve hacia la izquierda 20
m para ubicarse en el punto Q y luego se traslada 70 m hacia la derecha hasta
ubicarse el punto R.
Ubica y etiqueta los
puntos Q y R en el dibujo (cada división es 10 m) y a partir de eso determina:
a.)
La posición inicial
b.)
La posición final
c.)
La distancia total recorrida
d.) El desplazamiento
a.) La posición inicial
Corresponde a la del punto P y que está
ubicada en el origen de coordenadas (0,0) m
b.) La posición final
Debe ser la del punto R, es decir 50 m a la
derecha (= + 50 m)
c.) La distancia total recorrida
Debe tomarse en cuenta toda la trayectoria
realizada sin importar la dirección, así se tiene
= 20 + 70 = 90 m.
d.) El desplazamiento
Sólo interesa la diferencia existente entre
las posiciones inicial y final, = + 50 – (0) = + 50 m, lo que
significa que el desplazamiento ha sido 50 m dirigidos hacia a la derecha
Ejemplo 3
Gorgue se encuentra en la ciudad de Azogues cuyas coordenadas son (-7,2) respecto al plano de coordenadas geográficas, y necesita llegar a un sitio en Cuenca con coordenadas (4, 6). ¿Cuál es la magnitud y dirección del vector desplazamiento entre dichas ciudades, considerando que la distancia que recorre el autobús está en km?
Opciones de respuesta:
A) 11.70 km; 19º58’59’
B) 13.60 km; 36º01’38’’
C) 13.60 km; 70º01’
se presenta una solución gráfica, se deja al estudiante la solución analítica. 
otro ejemplo
Un campesino, para movilizarse desde su casa al mercado del pueblo primero camina A (0,2 km al norte, 50 m al este); luego se dirige B (80 m en la dirección N30°O) para luego caminar otros C (30 m con un ángulo de 60° con respecto a la dirección desde el este hacia el norte. Expresa cada vector en su componente rectangular, geográfica y polar. Calcula la distancia de su casa a la iglesia. Se deja como tarea para el estudiante.
escala: 1=50m
La posición de un móvil es el punto del espacio donde se encuentra en un instante determinado, es decir, respecto a un sistema de referencia.
El módulo del vector posición es:
la unidad del módulo del vector de posición en el SI es el metro (m).En general podemos expresar el vector de
posición en función del tiempo que es la ecuación del movimiento. r = r(t) = x(t)i + y(t) j
Las ecuaciones de las componentes del
vector de posición en función del tiempo, x = x(t), y = y(t), son las ecuaciones
paramétricas de r.
Finalmente, si en una de las ecuaciones
paramétricas se despeja la variable tiempo y se sustituye en la otra, resulta
una función de x y de y. Es decir, se obtiene F (x, y) = 0, que es la ecuación
de la trayectoria.
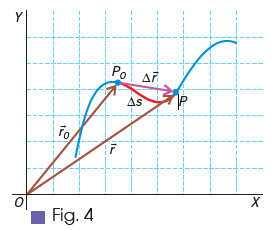
El vector desplazamiento, Δr entre dos puntos, Po y P, es el vector con origen en Po y extremo en P.
ejemplo de aplicaciónEl vector posición de una pelota que se
ha lanzado a canasta viene dado, en función del tiempo, por la expresión r =
3ti + (6t − 5t2) j, en unidades del SI.
a. Determinemos
la posición del móvil en los instantes t = 0 s, t = 0,50 s y t = 1,0 s.
b. Calculemos
la distancia del móvil respecto al origen de coordenadas en t = 1,0 s.
c. Calculemos
el vector desplazamiento entre los instantes de t = 0,50 s y t = 1,0 s
d. Determinemos
la ecuación de la trayectoria y dibujémosla.
COMPRENSIÓN. Para hallar el valor del
vector de posición en un instante dado, basta con sustituir el valor del tiempo
en la ecuación del movimiento. La distancia al origen será el módulo del vector
de posición, mientras que el desplazamiento entre dos instantes es la
diferencia entre los vectores de posición.
DATOS. r = 3ti + (6t - 5t2) j,
en unidades del SI.
a. Hallamos el vector de posición en los
instantes propuestos:
Resolver
Una canica se muestra sobre una superficie
plana. la expresión del vector posición en función del tiempo es: r = (2t + 2)
i + (4t4 – 3t2) j, en unidades del SI. Halla:
- a) La posición en los instantes t = 0 s y
t = 2 s.
- b) El vector desplazamiento entre estos
instantes.
Una hormiga que está en la posición (5, 0)
se mueve a la posición (2, 2). Calcula la diferencia entre el vector de
posición final y el inicial.
—¿Cómo se llama esta diferencia? ¿En qué
caso puede coincidir el espacio recorrido con el módulo de la diferencia
anteriormente calculada?
Rapidez y velocidad. Valores medios e instantáneos.
- Diferenciar rapidez y velocidad, a partir de la conceptualización escalar o vectorial
- Determinar valores medios e instantáneos de las magnitudes cinemáticas, desde las especificaciones del tiempo conocidas.
Rapidez y velocidad son dos magnitudes cinemáticas que suelen confundirse con frecuencia.
La rapidez es una
magnitud escalar que relaciona la distancia recorrida con el tiempo.
La velocidad es una
magnitud vectorial que relaciona el cambio de posición (o desplazamiento) con el tiempo.
El sitio http://www.educaplus.org/movi/2_5velocidad.html ofrece un refuerzo de los conceptos revisados, así como simulaciones para que el estudiante las revise referentes a rapidez y velocidad
2.5 Resistencia del aire
Destrezas con criterios de desempeño
Integrar el concepto de velocidad terminal, desde la descripción del efecto de la resistencia del aire sobre el movimiento de un objeto.
Precisiones para la enseñanza y el aprendizaje
Todos damos por hecho que cuando un objeto es soltado o lanzado desde una altura determinada, su velocidad irá progresivamente aumentando como resultado del efecto de la gravedad. No obstante, esto no sucede en la realidad, ya que el aire ofrece una resistencia al movimiento de un objeto y por lo tanto va reduciendo el efecto de la fuerza de la gravedad hasta anularla completamente, dando como resultado que la velocidad se estabiliza en un valor conocido como velocidad terminal, la misma que varía dependiendo de la posición y la masa del objeto que desciende libremente. Como referencia tenemos estos datos encontrados en http://ciencianet.com/paraca.html
LECCION # 4
1. El récord mundial vigente para la prueba de atletismo de 100 m planos es 9,59 s. conseguido por el atleta jamaiquino Usain Bolt. Determina el valor de la rapidez máxima que pudo alcanzar (suponiendo que la aceleración del atleta es constante) y exprésala en km/h. Realiza un comentario al respecto.
SOLUCIÓN:
EL valor de la rapidez máxima es sumamente alto si se toma en cuenta que correspondería al
de un vehículo moviéndose casi a 75 km/h.
2. Un avión necesita alcanzar una rapidez mínima de despegue de 250 km/h, para lo cual debe recorrer una pista de 1400 m. Calcula el valor de la aceleración del avión y el tiempo empleado en su recorrido de despegue sobre la pista.
SOLUCIÓN:
Los 250 km/h de rapidez final corresponden a 69,4 m/s y el avión parte del reposo por su puesto.
3. Se suelta desde lo alto de un puente una piedra que llega al río en 2,4 s. Establece la altura del puente y la rapidez con la que llega al agua.
SOLUCIÓN:
v = 24,0 m/s
4. Una moneda es lanzada verticalmente hacia arriba. Si alcanza una altura máxima de 60 cm, ¿con qué velocidad fue lanzada?, ¿en qué tiempo regresará a la mano de quien la lanzó?SOLUCIÓN:
El valor calculado sólo expresa el tiempo de duración de la subida, y como se debe entender que el tiempo de descenso es el mismo porque la trayectoria es simétrica, el tiempo total sería entonces:
t = 0,35s + 0,35s
t = 0,70s
CLIC PARA CONTINUAR A MOVIMIENTO EN DOS DIMENCIONES


.png)






.png)








.png)
.png)
.png)
