DESTREZA: Reconocer la importancia del estudio de la Física como asignatura de carácter experimental desde su incidencia en el desarrollo de la vida cotidiana y su relación con otras ciencias.
- Enliste todos los objetos modernos que simplifican nuestras tareas gracias a la tecnología y relacione como la física ha posibilitado su desarrollo.
- Responda ¿Por qué estudiar física?
- Vea el vídeo y reflexione con ejemplos, como la física se relaciona con otras ciencias. Por ejemplo en Biología, al estudiar la presión sanguínea y en Astronomía al estudiar la gravitación y las leyes de Kepler.
"Ciencia y tecnología: también son distintas entre sí. La ciencia se
ocupa de reunir conocimientos y organizarlos. La tecnología permite al
hombre usar esos conocimientos para fines prácticos, y proporciona las herramientas
que necesitan los científicos en sus investigaciones. Pero la tecnología puede resultar
útil o perjudicial. Por ejemplo, contamos con la tecnología para extraer combustibles
fósiles del suelo, para después quemarlos y producir energía. La producción de energía
ha beneficiado a nuestra sociedad de incontables maneras; por otro lado, pone
en peligro al ambiente. Es tentador echar la culpa a la tecnología misma por
problemas como la contaminación, el agotamiento de los recursos; sin embargo,
estos problemas no son causados por la tecnología, ya que los humanos somos
responsables de cómo se usa". HEWITT, PAUL G., Física conceptual, México,
Pearson, 1999.
CLIC PARA ACCEDER A PRUEBA DE DIAGNOSTICO. Imprima, desarrolle y presente a su profesor hasta el viernes 27 de septiembre de 2019. valido para un aporte.LA FÍSICA EN NUESTRO ENTORNO
- Relación de la física con otras ciencias.
- Sistemas físicos
- Sistema internacional de unidades
- Conversión de unidades
- La notación científica
- La teoría de errores
MAGNITUDES VECTORIALES Y ESCALARES
-Vectores.- Definición y ejemplos
-Componentes rectangulares
-Componentes polares
-Componentes geográficas
TRIGONOMETRÍA
-Conceptos trigonométricos
-Funciones trigonométricas
-Resolución de triángulos rectángulos
- Sistemas físicos
- Sistema internacional de unidades
- Conversión de unidades
- La notación científica
- La teoría de errores
MAGNITUDES VECTORIALES Y ESCALARES
-Vectores.- Definición y ejemplos
-Componentes rectangulares
-Componentes polares
-Componentes geográficas
TRIGONOMETRÍA
-Conceptos trigonométricos
-Funciones trigonométricas
-Resolución de triángulos rectángulos
Ver el vídeo que es la física y áreas de estudio
Sistemas físicos
Un sistema físico es un agregado de objetos o entidades materiales entre cuyas partes existe una conexión o interacción o un modelo matemático de tipo causal (aunque no necesariamente determinista o causal en el sentido de la teoría de la relatividad). Todos los sistemas físicos se caracterizan por:
- Tener una ubicación en el espacio-tiempo.
- Tener un estado físico definido sujeto a evolución temporal.
- Poderle asociar una magnitud física llamada energía.
Sistemas
físicos en relación al entorno
Los sistemas físicos pueden ser
abiertos, cerrados o aislados, según que realicen o no intercambios con su
entorno:
Un
sistema abierto es un sistema que recibe flujos
(energía y materia) de su entorno, pueden realizar el trabajo de mantener sus
propias estructuras e incluso incrementar su contenido de información. El hecho
de que los seres vivos sean sistemas estables capaces de mantener su estructura
a pesar de los cambios del entorno requiere que sean sistemas abiertos.
Un
sistema cerrado sólo intercambia energía con su
entorno, en un sistema cerrado el valor de la entropía es máximo compatible con
la cantidad de energía que tiene.
Un
sistema aislado no tiene ningún intercambio con
el entorno.
LA FÍSICA es la ciencia que tiene por objeto el estudio de la materia, la energía, sus propiedades e interacciones. Podemos decir que la Física intenta una explicación del universo, en lo que corresponde tanto al macrocosmos como al microcosmos. Hasta el siglo XVI, la Física no existió como ciencia independiente sino que fue tratada como parte de la Filosofía, con Galileo Galilei, la Física adquiere plenamente su dimensión experimental.
MAGNITUDES
Para conocer el entorno físico es necesario distinguir las características y propiedades de los objetos o fenómenos naturales y asignarles un valor. La cualidad que podemos medir de una propiedad física es una magnitud, se clasifican en: fundamentales y derivadas.
LA MEDIDA
Es necesario medir las propiedades de los objetos y fenómenos para detectar las diferencias. La medida es la comparación entre dos cualidades semejantes de dos objetos, para determinar cuántas veces se repite dicha cualidad, cuando uno de ellos se toma como base de comparación (patrón)
Todo patrón de medida se instituye por medio de una convención que las naciones adoptan para efectuar mediciones comunes y evitar confusiones. Los acuerdo sobre la selección y uso de los patrones se establecen en reuniones internacionales de la Conferencia General de Pesos y Medidas, con sede en París.
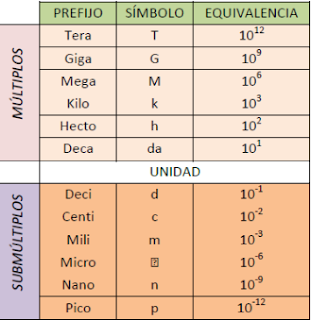
En la actualidad se cuenta con un Sistema Internacional de unidades, cuyas siglas oficiales son SI. Este sistema es un conjunto de unidades de medición que se emplea de forma cotidiana en la mayoría de los países del planeta. En el SI existen siete unidades fundamentales, 141 derivadas, que se forman combinando las unidades fundamentales por medio de expresiones algebraicas, dos unidades suplementarias que corresponden a las magnitudes de ángulo plano, de ángulo solido y cuyos nombres son radian (rad) y estero radian (sr).
Además del SI, existen otros sistemas de medidas sin embargo son pocos los países que lo emplean. Un ejemplo es el sistema técnico inglés, que se utiliza en Estados Unidos, Australia, Myanmar (antes Birmania) y Liberia entre otros países. Las unidades básicas de este sistema son el pie, ft (0,3048 m), para la longitud; la libra, lb (0,4535) kg), para la masa; y el segundo para el tiempo.
CONVERSIÓN DE UNIDADES
Un método muy practico para la conversión de unidades el de factores de conversión. consiste en multiplicar el dato por fracciones que expresan la equivalencia entre la unidad deseada y la unidad del dato.
Lo que tengo x lo que quiero = lo que quiero
Unidad de lo que tengo
Clic para acceder al archivo de trabajo física
La notación científica se utiliza para facilitar la expresión de cantidades muy grandes o muy pequeñas, y los cálculos que se derivan de ellas. Los números se expresan mediante una parte entera de una cifra (diferente de cero), una parte decimal y una potencia de 10 de exponente entero.
Formato de la Notación Científica
video de aplicación de funciones trigonométricas
ver vídeo suma de vectores método gráfico (paralelogramo)
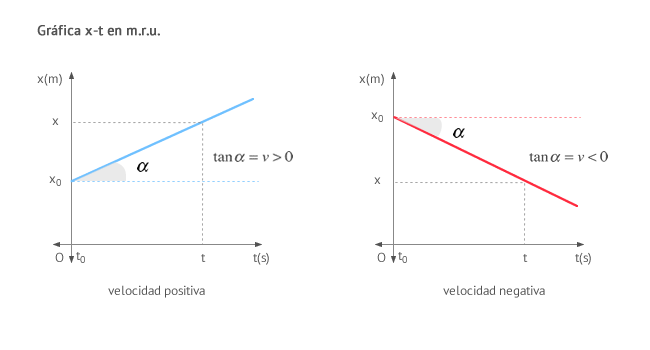
CONVERSIÓN DE UNIDADES
Un método muy practico para la conversión de unidades el de factores de conversión. consiste en multiplicar el dato por fracciones que expresan la equivalencia entre la unidad deseada y la unidad del dato.
Lo que tengo x lo que quiero = lo que quiero
Unidad de lo que tengo
Por ejemplo, transformar 72km/h a ft/s (pies/segundo)
72 km x 1000 m x 100 cm x 1ft __ x 1h _ x 1min_ = 65,62 ft/s
h 1km 1m 30,48 cm 60 min 60s
1m = 100 cm
1ft = 12 pulgadas (in) = 30,48 cm
1 kg = 1000 g
1 tonelada (T) = 1000 kg
1 kg = 2,2 lb
1 lb = 16 oz (onzas)
1 in (pulgada) = 2,54 cm
1 milla(mi) = 1,609 km
1slug (unidad de masa en el sistema británico) =14,59 kg
1 lt (litro) = 1dm3
Cuadro de magnitudes fundamentales
Las magnitudes derivadas más útiles que se exponen en la siguiente tabla:
72 km x 1000 m x 100 cm x 1ft __ x 1h _ x 1min_ = 65,62 ft/s
h 1km 1m 30,48 cm 60 min 60s
1m = 100 cm
1ft = 12 pulgadas (in) = 30,48 cm
1 kg = 1000 g
1 tonelada (T) = 1000 kg
1 kg = 2,2 lb
1 lb = 16 oz (onzas)
1 in (pulgada) = 2,54 cm
1 milla(mi) = 1,609 km
1slug (unidad de masa en el sistema británico) =14,59 kg
1 lt (litro) = 1dm3
Cuadro de magnitudes fundamentales
La notación científica se utiliza para facilitar la expresión de cantidades muy grandes o muy pequeñas, y los cálculos que se derivan de ellas. Los números se expresan mediante una parte entera de una cifra (diferente de cero), una parte decimal y una potencia de 10 de exponente entero.
Formato de la Notación Científica
La notación científica de un número real es su expresión como el producto de un número mayor o igual que 1 y menor que 10, por una potencia de 10. La forma general de un número escrito a partir de su notación científica es: k x 10ⁿ donde 1 <= k <10 y n ⥺ N
Además, n es negativo cuando corresponde a la expresión de una cantidad muy pequeña y n es positivo cuando se relaciona con una cantidad muy grande.
Aplicando la notación científica a la escritura del diámetro del glóbulo rojo y la distancia de la Tierra al Sol, se obtiene lo siguiente:
0,0065 mm = 6,5 x 10⁻³
Hay tres lugares entre el lugar de la coma y el 6. Por ello, el exponente de la potencia es -3.
150 000 000 000 m = 1,5 x 10¹¹
Hay once lugares entre el final del número y el 1. Por ello, el exponente de la potencia es +11.
Veamos algunos ejemplos:
MAGNITUDES VECTORIALES Y ESCALARES
Vectores.- Definición y ejemplos
para denotar un vector usamos gráficamente la flecha, donde la saeta nos indica la dirección y la medida de su longitud, el modulo; un vector necesariamente esta emplazado en un sistema de referencia.
vídeo, representación de vectores en el plano https://www.youtube.com/watch?v=hUFfjHntdUs
VECTORES EN EL PLANO
Componentes rectangulares.
Todo vector puede ser expresado por sus componentes horizontal y vertical con respecto aun sistema de referencia. Para indicar la dirección de la componente en (x) usamos (i) como unidad del vector, con el signo positivo si va a la derecha y negativo si va a la izquierda; para la componente en (y) usamos (j), con signo positivo si va hacia arriba y negativo si va hacia abajo.
Para denotar un vector usamos una saeta sobre la letra que indica el vector y dado por sus componentes tenemos
Coordenadas polares
Las coordenadas polares indican el modulo y la dirección, dado por la forma,
siendo A el módulo y q el angulo formado por el vector con respecto al eje de x(+)
Coordenadas geográficas
Las coordenadas geográficas indican el modulo y la dirección expresado en función de los puntos cardinales.
En este caso
ver vídeo aplicación de las funciones trigonométricas
Además, n es negativo cuando corresponde a la expresión de una cantidad muy pequeña y n es positivo cuando se relaciona con una cantidad muy grande.
Aplicando la notación científica a la escritura del diámetro del glóbulo rojo y la distancia de la Tierra al Sol, se obtiene lo siguiente:
0,0065 mm = 6,5 x 10⁻³
Hay tres lugares entre el lugar de la coma y el 6. Por ello, el exponente de la potencia es -3.
150 000 000 000 m = 1,5 x 10¹¹
Hay once lugares entre el final del número y el 1. Por ello, el exponente de la potencia es +11.
Veamos algunos ejemplos:
Número
|
¿Notación Científica?
|
Explicación
|
1,85 x 10-2
|
sí
|
-2 es un entero
|
1,5 x 101/2
|
no
|
no es un entero
|
0,82 x 1014
|
no
|
0.82 no es ≥ 1
|
10 x 103
|
no
|
10 no es < 10
|
MAGNITUDES VECTORIALES Y ESCALARES
Vectores.- Definición y ejemplos
- Reflexión
Cuando alguien nos pide que le alcancemos un
kg de azúcar o un litro de leche, no hay problema, lo podemos hacer, pero
cuando nos pide que ayudemos a mover un mueble, necesitamos saber cuánta fuerza
necesitamos realizar y en qué dirección deberíamos hacerlo.
En los dos casos hablamos de magnitudes físicas. En el primer caso: el de los kilogramos de azúcar o el litro de leche , se trata de magnitudes escalares, donde para definirlo solo es necesario la cantidad, lo que denominamos módulo. En el segundo caso, el de la fuerza, se trata de una magnitud vectorial, en donde además del modulo necesitamos definir la dirección.
Principales magnitudes
|
|
Escalares
|
Vectoriales
|
Longitud
|
Velocidad
|
Área
|
Aceleración
|
Volumen
|
Fuerza
|
Rapidez
|
Corriente
eléctrica
|
Masa
|
Intensidad
de campo gravitacional
|
Energía
|
Intensidad
de campo eléctrico
|
En física llamamos vector a la magnitud que posee modulo,
dirección y su unidad correspondiente; en la dirección está incluido el sentido.
Además es necesario definir mediante sus coordenadas en un sistema de referencia ya sea por sus componentes rectangulares,
polares, geométricas o por el vector unitario.
Un
vector fijo es
un segmento orientado que va del punto A (origen) al
punto B (extremo).Los vectores, en física, nos sirven para representar una
magnitud física como la velocidad o la fuerza.
Un vector tiene
- Origen o Punto de Aplicación: es el punto
exacto sobre el que actúa el vector.
- Módulo: es la longitud o tamaño del
vector. Para saber el módulo de un vector es necesario conocer el punto inicial
y final del vector (origen y extremo). Para calcular el módulo se mide desde el
origen hasta el extremo.
- Dirección: viene dada por la orientación en el espacio de
la recta que lo contiene. La recta que contiene el vector es su dirección, pero
también es el ángulo que tiene el vector con respecto al eje de referencia. Si
el eje de referencia es horizontal, el ángulo que forma el vector, con la
horizontal, será la dirección.
- Sentido: se indica mediante una punta de flecha situada en el extremo del vector, indicando hacia que lado se dirige el vector.
- Sentido: se indica mediante una punta de flecha situada en el extremo del vector, indicando hacia que lado se dirige el vector.
VECTORES EN EL PLANO
- Componentes rectangulares
- Componentes polares
- Componentes geográficas
- Suma de vectores: método del polígono, del paralelogramo y analítico.
- Conceptos trigonométricos
- Funciones trigonométricas
- Resolución de triángulos rectángulo
Componentes rectangulares.
Todo vector puede ser expresado por sus componentes horizontal y vertical con respecto aun sistema de referencia. Para indicar la dirección de la componente en (x) usamos (i) como unidad del vector, con el signo positivo si va a la derecha y negativo si va a la izquierda; para la componente en (y) usamos (j), con signo positivo si va hacia arriba y negativo si va hacia abajo.
Para denotar un vector usamos una saeta sobre la letra que indica el vector y dado por sus componentes tenemos
Las coordenadas polares indican el modulo y la dirección, dado por la forma,
Las coordenadas geográficas indican el modulo y la dirección expresado en función de los puntos cardinales.
En este caso
ver vídeo suma de vectores método gráfico (paralelogramo)
Ver vídeo suma de vectores método gráfico (polígono)
Suma de vectores método analítico
Movimiento en una dimensión
Identificar la posición y el desplazamiento de un objeto (considerado
puntual) que se mueve, a lo largo de una trayectoria rectilínea, en un sistema
de referencia establecida. REF. (CN.F.5.1.1.)
CN.F.5.1.2. Explicar, por medio de la experimentación de un objeto y el
análisis de tablas y gráficas, que el movimiento rectilíneo uniforme implica
una velocidad constante.
Registrar gráficamente que, en el caso particular de que la trayectoria sea
un círculo, la aceleración normal se llama aceleración central centrípeta.
REF. (CN.F.5.1.12.)
CN.F.5.1.26. Determinar que el lanzamiento vertical y la caída libre son
casos concretos del movimiento unidimensional con aceleración constante (g)
mediante ejemplificaciones y utilizar las ecuaciones del movimiento vertical en
la solución de problemas.
Describir el movimiento de proyectiles en la superficie de la Tierra,
mediante la determinación de las coordenadas horizontal y vertical del objeto
para cada instante del vuelo y de las relaciones entre sus magnitudes
(velocidad, aceleración, tiempo); determinar el alcance horizontal y la altura
máxima alcanzada por un proyectil y su relación con el ángulo de lanzamiento
REF. (CN.F.5.1.29.)
3 MOVIMIENTO:
3.1 Posición y desplazamiento.- Posición, trayectoria, distancia y desplazamiento.- definición y gráficas
3.2 Rapidez y velocidad:
3.3 Velocidad media e instantánea.
3.4 Movimiento rectilíneo uniforme
3.5 Aceleración
3.6 Movimiento rectilíneo uniformemente variado. - Movimiento horizontal y Caída libre
3.7 Movimiento de proyectiles.
POSICIÓN Y DESPLAZAMIENTO
Es importante señalar la diferencia que hay entre espacio recorrido y desplazamiento ya que son, en general, conceptos distintos que se suelen confundir. El espacio o distancia recorrido es una magnitud escalar que se mide sobre la trayectoria. El desplazamiento es una magnitud vectorial que sólo depende de la posición inicial y final del cuerpo y es independiente de la trayectoria
Trayectoria.- corresponde al camino seguido por una partícula o un cuerpo que se desplaza.
3.1 Posición y desplazamiento.- Posición, trayectoria, distancia y desplazamiento.- definición y gráficas
3.2 Rapidez y velocidad:
3.3 Velocidad media e instantánea.
3.4 Movimiento rectilíneo uniforme
3.5 Aceleración
3.6 Movimiento rectilíneo uniformemente variado. - Movimiento horizontal y Caída libre
3.7 Movimiento de proyectiles.
POSICIÓN Y DESPLAZAMIENTO
Es importante señalar la diferencia que hay entre espacio recorrido y desplazamiento ya que son, en general, conceptos distintos que se suelen confundir. El espacio o distancia recorrido es una magnitud escalar que se mide sobre la trayectoria. El desplazamiento es una magnitud vectorial que sólo depende de la posición inicial y final del cuerpo y es independiente de la trayectoria
Posición.- Es un punto en el espacio respecto a un sistema de referencia. representa el vector
que une el lugar ocupado por el cuerpo con el origen del sistema de
referencia
La ecuación de posición o ecuación de trayectoria representa el vector de posición en función del tiempo. Su expresión, en coordenadas cartesianas y en dos dimensiones viene dada por:
La ecuación de posición o ecuación de trayectoria representa el vector de posición en función del tiempo. Su expresión, en coordenadas cartesianas y en dos dimensiones viene dada por:
La rapidez es una magnitud escalar que relaciona la distancia recorrida con el tiempo, representa el modulo de la velocidad.
La velocidad es una magnitud vectorial que relaciona el cambio de posición (o desplazamiento) con el tiempo.
En el Sistema Internacional, la unidad para la rapidez media es el m/s (metro por segundo).
En el Sistema Internacional, la unidad para la rapidez media es el m/s (metro por segundo).
clic para acceder al vídeo: Cinemática, velocidad, desplazamiento, distancia, gráficas
MOVIMIENTO RECTILÍNEO UNIFORME
Cuando un cuerpo mantiene su velocidad constante, es decir, recorre distancias iguales en tiempos iguales, decimos que su movimiento es rectilíneo uniforme, sintetizado en las siglas MRU.
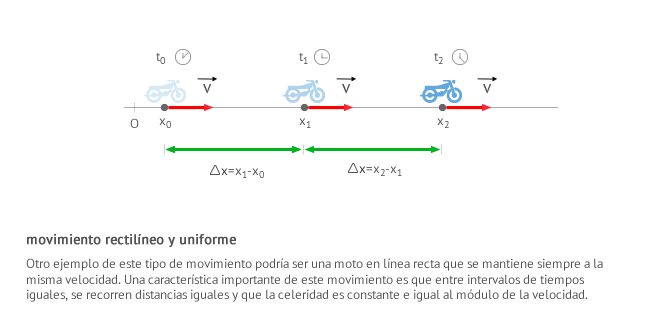Velocidad constante implica rapidez constante y movimiento rectilíneo, ya que al tener velocidad constante su dirección también sera constante y por tanto su movimiento sera rectilíneo.
En el movimiento rectilíneo la velocidad instantánea es igual a su velocidad media.
es decir:
V= ∆r/t
y su rapidez
V= d/t
Ejemplo. el auto tiene una velocidad constante V=10 m/s lo que quiere decir que cada segundo recorre 10 m.
Ecuaciones y gráficas
Posición.- Su unidad en el Sistema Internacional (S.I.) es el metro (m) y se obtiene por medio de la siguiente expresión:
xo es la posición inicial.
v es la velocidad que tiene el cuerpo a lo largo del movimiento.
t es el intervalo de tiempo durante el cual se mueve el cuerpo.
MOVIMIENTO RECTILÍNEO UNIFORME
Cuando un cuerpo mantiene su velocidad constante, es decir, recorre distancias iguales en tiempos iguales, decimos que su movimiento es rectilíneo uniforme, sintetizado en las siglas MRU.
En el movimiento rectilíneo la velocidad instantánea es igual a su velocidad media.
es decir:
V= ∆r/t
y su rapidez
V= d/t
Ejemplo. el auto tiene una velocidad constante V=10 m/s lo que quiere decir que cada segundo recorre 10 m.
Ecuaciones y gráficas
Posición.- Su unidad en el Sistema Internacional (S.I.) es el metro (m) y se obtiene por medio de la siguiente expresión:
xo es la posición inicial.
v es la velocidad que tiene el cuerpo a lo largo del movimiento.
t es el intervalo de tiempo durante el cual se mueve el cuerpo.
En aquellos casos en los que la posición inicial es cero ( x0 = 0 ), la distancia recorrida y la posición coinciden, y su valor es:
Un bus avanza con MRU a 72 km/h. determinar el tiempo que tarda en avanzar 200 m
Mario y Luis se mueven con MRU y van al encuentro. Calcular el tiempo que emplean para encontrarse; sabiendo que Mario va a 10 m/s y Luis a 5 m/s, y la distancia de separación es de 300 m.
ver solución
1. Pedro va al colegio caminando desde su casa. La distancia que debe recorrer es de 410 m. Si tarda 6 min 24 s en llegar, ¿cuál es la velocidad de Pedro?
Caraco l 50 m/h
Tortuga 70 m/h
1. Pedro va al colegio caminando desde su casa. La distancia que debe recorrer es de 410 m. Si tarda 6 min 24 s en llegar, ¿cuál es la velocidad de Pedro?
2.
Un ciclista se encuentra en el kilómetro 25 de una etapa de 115 km. ¿Cuánto
tiempo tardará en llegar a la meta si rueda a una velocidad de 60 km/h?
3.
Si los animales tuvieran sus propios juegos olímpicos, según estos datos, ¿cuál
obtendría la medalla de oro en una carrera de 200 metros lisos?
Oso perezoso 0,2 km/h Caraco l 50 m/h
Tortuga 70 m/h
4. Un ave vuela a una velocidad constante de 15 m/s. a. Confecciona una tabla que recoja las posiciones del ave cada 5 s durante un vuelo de 30 s. b. Dibuja en tu cuaderno la gráfica posición tiempo del ave a partir de los valores registrados en la tabla.
