PAQUETES CONTABLES TERCER CURSO

PAQUETES CONTABLES TERCER CURSO
CONTENIDOS DEL CURSO:
 OBJETIVOS:

• Manejar la hoja electrónica a fin de elaborar documentos administrativos y contables.
• Utilizar el programa tributario con el objetivo de dar cumplimiento a las obligaciones de los contribuyentes.
• Efectuar el control contable utilizando los diferentes módulos del paquete.
• Automatizar el proceso contable y tributario a fin de optimizar tiempo y recursos. 

ACTITUDES VALORES Y NORMAS

• Demostrar creatividad en la elaboración de tareas aplicando destrezas y habilidades tecnológicas.
• Ser capaz de aplicar las fórmulas y funciones en el desarrollo de los cálculos y obtención de resultados.
• Siente Interés por presentar los documentos y formularios de forma responsable y puntual.
• Toma conciencia de la importancia que tiene el conocimiento contable para obtener información automatizada confiable.
• Valorar el cuidado y mantenimiento adecuado de los equipos y mobiliario del laboratorio.

BLOQUE 1:
NIVELACIÓN FORMULAS Y FUNCIONES EN EL PROCESO CONTABLE:

Ver el vídeo y presentar informe:

• Cortar, copiar, pegar y mover
• Barra de formulas
• Operadores aritméticos
• Presente las fórmulas utilizadas: Suma, Promedio, Máximo y Mínimo
• Qué es una referencia de celda.
• Tipos de referencia de celda: referencia relativa referencia absoluta.

BLOQUE 2
SOFTWARE TRIBUTARIO:

• DIMM: definición, objetivos y utilidad.
• Formularios: tipos y aplicación.
• Anexos: tipos y aplicación.Desarrolle estos contenidos en el cuaderno de trabajo para lo cual debe acceder a estos vínculos.

Clic para acceder a la página y consultar información del DIMM formulario
Clic para ir a la página y descargar el DIMM formulario

BLOQUE 3
APLICACIÓN DEL A HOJA ELECTRÓNICA AL PROCESO CONTABLE :

• COMPONENTES DE UN ROL DE PAGOS Y ROL DE PROVISIONES SOCIALES.
• SOPORTES DE CONTABILIDAD: GENERALIDADES Y CLASIFICACIÓN
• SOPORTES DE CONTABILIDAD INTERNOS:
• REGISTRO CONTABLE.- CONCEPTO, TIPOS Y EJEMPLOS
• ELABORAR UN ROL DE PAGOS
• AUTOMATIZAR UNA FACTURA
• ELABORAR UN REGISTRO DE INGRESOS Y GASTOS

BLOQUE 4
AUTOMATIZACIÓN DE DOCUMENTOS CONTABLES:

• MOVIMIENTOS CAJA – BANCOS.
• GESTIÓN DE INVENTARIO Y STOCK
• MANEJO DE KARDEX Y MÉTODOS DE CONTROL DE EXISTENCIAS.

BLOQUE 5
AUTOMATIZACIÓN DE DOCUMENTOS CONTABLES:
Trabajando con funciones II

• Funciones matemáticas: Suma, Sumar.si, Contar 
• Funciones estadísticas: Max, Min, Contar.si 
• Funciones de tiempo: Ahora() 
• Funciones lógicas: Si(), 
• Funciones de búsqueda: BurcarV(), BurcarH() 

Objetivos del tema: Este tema se dedicará al repaso de las funciones vistas en temas anteriores, aunque la dificultad de los ejercicios es mayor. 
Duración del tema: 4 sesiones de 55 minutos 
Nivel de dificultad: Alta
BLOQUE 6
AUTOMATIZACIÓN DE DOCUMENTOS CONTABLES:

• Contabilidad: Proceso contable automatizado.

-------------------------------------------------------------------------------------------------------------------------

MATERIA BLOQUE 1
Usar funciones anidadas en una fórmula

Excel nos permite crear fórmulas que contienen varias funciones, y la manera de hacerlo es utilizando una función como el argumento de la otra. A este uso de las funciones se le conoce como anidación.

Por ejemplo, supongamos que tenemos las 3 notas de cuatro alumnos y que todas pesan igual. No obstante, algunos alumnos no pudieron rendir el examen 3 por motivos personales, por lo cual se les tomará otro examen posteriormente. Si se desea conocer el promedio de los alumnos que si han rendido los 3 exámenes, se utilizará la función SI y dentro de ella se calculará el promedio, solo si ninguna de estas celdas se encuentra en blanco. Caso contrario el valor queda vacío: Deber, pasar a Excel la tabla de imagen.

FUNCIONES CONDICIONALES

PROMEDIO.SI.CONJUNTO en Microsoft Excel.

Descripción

Devuelve el promedio (media aritmética) de todas las celdas que cumplen múltiples criterios.

Sintaxis

PROMEDIO.SI.CONJUNTO(rango_promedio; rango_criterio1; criterio1; [rango_criterio2; criterio2];...)

Rango_promedio Obligatorio. Una o más celdas cuyo promedio se desea obtener que incluyan números, o nombres, matrices o referencias que contengan números.

Rango_criterio1; rango_criterio2;… Rango_criterio1 es obligatorio, los demás rangos de criterios son opcionales. De 1 a 127 rangos en los que se van a evaluar los criterios asociados.

Criterio1; criterio2;… Criterio1 es obligatorio, los criterios siguientes son opcionales. De 1 a 127 criterios en forma de número, expresión, referencia de celda o texto que determinan las celdas cuyo promedio se va a calcular. Por ejemplo, los criterios pueden expresarse como 32, "32", ">32", "manzanas" o B4.

Nota: La función PROMEDIO.SI.CONJUNTO mide la tendencia central, que es la ubicación del centro de un grupo de números en una distribución estadística. Las tres medidas más comunes de tendencia central son las siguientes:

Promedio.- Es la media aritmética y se calcula sumando un grupo de números y dividiendo a continuación por el recuento de dichos números. Por ejemplo, el promedio de 2, 3, 3, 5, 7 y 10 es 30 dividido por 6, que es 5.

Mediana.- Es el número intermedio de un grupo de números; es decir, la mitad de los números son superiores a la mediana y la mitad de los números tienen valores menores que la mediana. Por ejemplo, la mediana de 2, 3, 3, 5, 7 y 10 es 4.

Moda.- Es el número que aparece más frecuentemente en un grupo de números. Por ejemplo, la moda de 2, 3, 3, 5, 7 y 10 es 3.

EJEMPLO

Si deseo obtener el promedio de los artículos que son rojos y además medianos, entonces tendré que agregar dos argumentos a la función PROMEDIO.SI.CONUNTO de la siguiente manera:

=PROMEDIO.SI.CONJUNTO(B2:B11;C2:C11;"Rojo";D2:D11;"Mediano")

LA FUNCIÓN SUMAR.SI.CONJUNTO EN EXCEL

La función SUMAR.SI.CONJUNTO en Excel nos permite sumar los valores de un rango de celdas que cumplen con varias condiciones. A diferencia de la función SUMAR.SI que permite un solo criterio, la función SUMAR.SI.CONJUNTO permite hasta 127 criterios.

Sintaxis

SUMAR.SI.CONJUNTO(rango_suma; rango_criterios1; criterios1; [rango_criterios2; criterios2];...)

Rango_suma (obligatorio): El rango de celdas que contiene los valores a sumar. 

Rango_criterios1 (obligatorio): El rango de celdas que será evaluado por el Criterio1. 

Criterio1 (obligatorio): El criterio que deben cumplir las celdas del Rango_criterios1. 

Rango_criterios2 (opcional):El segundo rango de celdas que será evaluado por el Criterio2.

Criterio2 (opcional): El criterio que deben cumplir las celdas del Rango_criterios2. 

Los valores de las celdas del rango_suma se sumarán solamente si cumplen con los criterios especificados. Solo el Rango_criterios1 y Criterio1 son obligatorios, a partir de ellos podemos especificar múltiples combinaciones de Rango_criterio y Criterio hasta un máximo de 127.

EJEMPLO

Cantidad vendida	Producto	Vendedor
5	Manzanas	Juan
4	Manzanas	Leticia
15	Alcachofas	Juan
3	Alcachofas	Leticia
22	Plátanos	Juan
12	Plátanos	Leticia
10	Zanahorias	Juan
33	Zanahorias	Leticia

Descripción.

Agrega el número de productos que comienzan con A y fueron vendidos por Juan. 

Formula

=SUMAR.SI.CONJUNTO(A2:A9; B2:B9; "=A*"; C2:C9; "Juan") Resultado 15

Descripción.

Agrega el número de productos que no son plátanos y que fueron vendidos por Juan.

Formula 

=SUMAR.SI.CONJUNTO(A2:A9; B2:B9; "<>Plátanos"; C2:C9;"Juan") Resultado 30

LA FUNCIÓN SI EN EXCEL

La función SI en Excel es parte del grupo de funciones Lógicas y nos permite evaluar una condición para determinar si es falsa o verdadera. La función SI es de gran ayuda para tomar decisiones en base al resultado obtenido en la prueba lógica.

Sintaxis

=SI(prueba_lógica;[valor_si_verdadero];[valor_si_falso])

Prueba_lógica (obligatorio): Expresión lógica que será evaluada para conocer si el resultado es VERDADERO o FALSO.

Valor_si_verdadero (opcional): El valor que se devolverá en caso de que el resultado de la Prueba_lógica sea VERDADERO.

Valor_si_falso (opcional): El valor que se devolverá si el resultado de la evaluación es FALSO.

La Prueba_lógica puede ser una expresión que utilice cualquier operador lógico o también puede ser una función de Excel que regrese como resultado VERDADERO o FALSO.

Los argumentos Valor_si_verdadero y Valor_si_falso pueden ser cadenas de texto, números, referencias a otra celda o inclusive otra función de Excel que se ejecutará de acuerdo al resultado de la Prueba_lógica.

EJEMPLO

=SI(E7="Si";F5*0,0825;0)

En este ejemplo, la fórmula en F7 dice lo siguiente: SI(E7 = "Sí", calcula la cantidad total con F5 * 8,25 %; en caso contrario, no hay ningún impuesto sobre las ventas, por lo que se devuelve 0)

Nota: Si va a usar texto en fórmulas, tendrá que escribir el texto entre comillas (por ejemplo, "Texto").

-----------------------------------------------------------------------------------------------------------------------------

CONTAR.SI.CONJUNTO en Excel nos permite contar los elementos de un rango que cumplen con los criterios definidos. Esta función nos permite especificar hasta 127 criterios.

SINTAXIS

La función CONTAR.SI.CONJUNTO tiene dos argumentos obligatorios y los demás opcionales.

Rango_criterios1 (obligatorio): El rango de celdas que será evaluado con el Criterio1.

Criterio1 (obligatorio): El criterio con que se evaluará el Rango_criterios1.

Rango_criterios2 (opcional): El rango de celdas que será evaluado con el Criterio2.

Criterio2 (opcional): El criterio que evaluará el Rango_criterios2.

A partir del Rango_criterios2, todos los argumentos son opcionales y se permiten hasta 127 rangos y criterios a evaluar por la función CONTAR.SI.CONJUNTO. Cada rango especificado debe tener la misma cantidad de filas (o columnas) que los anteriores.
Ejemplo
Un negocio de artículos de computación y electrodomésticos cuenta con la siguiente tabla

y quiere saber cuantas veces el vendedor Juan López aparece en la misma, en el sector Electrodomésticos con ventas que superan los 200 $.

Como se ve los criterios son:

"Juan López"

"Electrodomésticos"

">200

entonces para responder a lo que el negocio quiere saber, se introduce la tabla en una Hoja de Excel y se usa la fórmula ( en la tabla se resaltan las filas que cumplen los 3 criterios)

nº de veces que aparece Juan López es 3

MATERIA BLOQUE 2 Y 3
COMBINAR LAS FUNCIONES SI. ERROR CON BUSCARV

Con la función SI.ERROR podemos tomar decisiones en caso de que el contenido o resultado de una celda se considere como error. Si no hay error se realizará la función o valor.
Sintaxis: SI.ERROR(Valor; valor en caso de error)
El argumento Valor es el valor, expresión o función que deseamos valorar para conocer si hay error. Este argumento es obligatorio.
El segundo argumento Valor en caso de error es el valor, expresión o función que se devolverá si el primer argumento es un error de los siguientes tipos: #N/A, #¡VALOR!, #¡REF!, #¡DIV/0!, #¡NUM!, #¿NOMBRE? o #¡NULO!
La función BUSCARV es una de las funciones más utilizadas para realizar búsquedas por lo que es inevitable que en algunas ocasiones no encontremos el valor buscado. En esos casos se mostrará el error #N/A, el cual no es tan amigable para el usuario, por lo que en esta ocasión te mostraré un método para personalizar dicho mensaje de error con la función SI. ERROR.
La siguiente imagen muestra el momento exacto en que la función BUSCARV realiza una búsqueda sobre el rango A2:A11 del nombre Dana que está indicado en la celda E1. Dicho nombre no existe dentro de la lista por lo que obtendremos como resultado el error #N/A.

Eliminar el error #N/A de la función BUSCARV

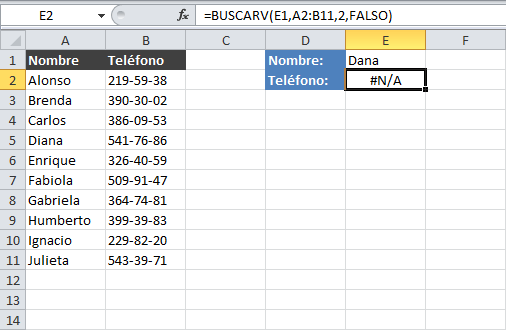
La manera más fácil de personalizar ese mensaje de error es utilizando la función SI. ERROR.

La función SI. ERROR tiene dos argumentos, el primero es el valor o expresión que va a evaluar y el segundo argumento es el valor que regresará en caso de que el primer argumento devuelva un error. En nuestro caso, el primer argumento será el resultado devuelto por la función BUSCARV tal como se muestra en la siguiente fórmula:

=SI.ERROR(BUSCARV(E1,A2:B11,2,FALSO), "Nombre no encontrado")

Esta fórmula evitará desplegar el mensaje de error #N/A devuelto por la función BUSCARV y en su lugar desplegará el mensaje “Nombre no encontrado”.

Por el contrario, si la función BUSCARV encuentra el valor buscado, entonces la función SI.ERROR no tendrá efecto alguno sobre el resultado. Observa la siguiente imagen donde hago la búsqueda del nombre “Diana” el cual existe dentro de la lista:

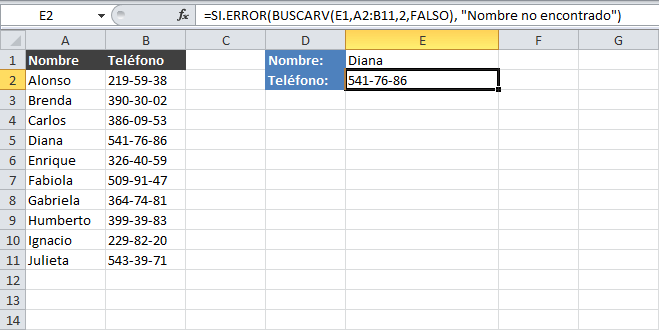
Recuerda que la función SI.ERROR solamente afectará el resultado de la fórmula en caso de detectar la presencia de un error. De esta manera, la función SI.ERROR nos ayuda a personalizar los mensajes de error de cualquiera de las funciones de Excel incluyendo la función BUSCARV.

BLOQUE 4

FUNCIÓN FILTRAR EN EXCEL

Los filtros en Excel nos permiten buscar un subconjunto de datos que cumpla con ciertos criterios. Generalmente todo comienza cuando tenemos un rango de celdas con información y queremos ver solamente aquellas filas que cumplen con ciertas condiciones.

Los filtros son una de las herramientas más útiles en Excel ya que nos permiten analizar los datos para conocer aquellos que cumplen con determinados criterios.

Todo usuario de Excel debe conocer a la perfección las opciones de filtrado que tenemos disponibles y por esa razón en esta ocasión revisaremos con detenimiento la manera en que funcionan los filtros en Excel.

En primer lugar, revisaremos las alternativas que tenemos para crear filtros.

Una de las opciones más utilizadas es crear una tabla lo cual agregará automáticamente los filtros.

Para crear una tabla, debes activar cualquier celda de los datos y en la pestaña Insertar hacer clic en el comando Tabla.

Eso abrirá el cuadro de diálogo Crear tabla que nos mostrará el rango de datos detectado automáticamente por Excel.

Si los datos tienen un encabezado, nos aseguramos de que el cuadro de selección esté activo y pulsamos el botón Aceptar.

Excel dará formato de tabla a los datos y eso incluirá los filtros que puedes observar en cada uno de los encabezados de columna.

Voy a pulsar el comando Deshacer para mostrarte la otra alternativa que tenemos para crear los filtros y es útil para esos casos en los que no queremos crear una tabla.

Solo debes asegurarte de activar cualquier celda de los datos y en la pestaña Inicio, dentro del grupo Edición, haré clic en el botón Ordenar y filtrar, y elegiré la opción Filtro y eso activará los filtros en los encabezados.

De nuevo pulsaré el comando Deshacer, para remover los filtros ya que voy a mostrarte que también podemos insertar los filtros con el atajo de teclado Ctrl + Shift + L y de inmediato se insertarán los filtros en los encabezados de columna.

Cualquiera de estos métodos nos ayudará a crear los filtros en cada uno de los encabezados de columna.

Algo que nunca debes olvidar es que las opciones de los filtros dependerán del tipo de dato que tiene cada columna y eso lo veremos a continuación.

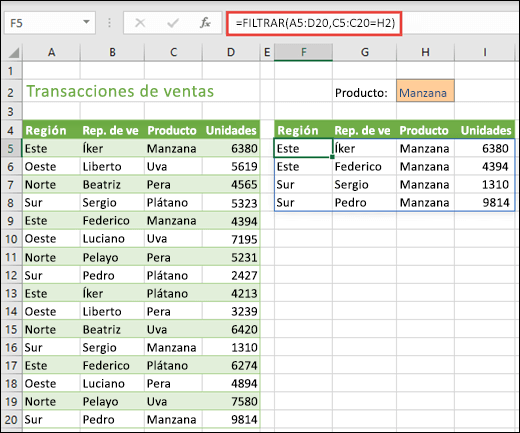
Utilizando la función FILTRAR

La función FILTRAR te permite filtrar un rango de datos en función de los criterios que definas.

En el ejemplo siguiente usamos la fórmula = filtro (A5: D20, C5: C20 = H2, “”) para devolver todos los registros de Apple, como está seleccionado en la celda H2, y si no hay manzanas, devuelva una cadena vacía (“”). ver vídeo

TRABAJO 1
Presenta un informe de este vídeo
descargar y realizar la plantilla

TRABAJO 2
Como llevar la contabilidad de un negocio pequeño con Excel

Llenar la plantilla de trabajo con las transacciones diarios y para los 12 meses del año. Continuación ingrese las formulas para automatizar los ingresos, egresos y gastos.

Las funciones a utilizar son: =texto; =sumar.si; =suma y operadores aritméticos. Mas los formatos de numero, moneda y fecha y presentación.

Descargar el archivo de trabajo

FÍSICA PRIMERO DE BACHILLERATO

“LA FÍSICA EN NUESTRO ENTORNO"

DESTREZA: Reconocer la importancia del estudio de la Física como asignatura de carácter experimental desde su incidencia en el desarrollo de la vida cotidiana y su relación con otras ciencias.

Ver el vídeo y reflexione:

• Enliste todos los objetos modernos que simplifican nuestras tareas gracias a la tecnología y relacione como la física ha posibilitado su desarrollo.
• Responda ¿Por qué estudiar física?
• Vea el vídeo y reflexione con ejemplos, como la física se relaciona con otras ciencias. Por ejemplo en Biología, al estudiar la presión sanguínea y en Astronomía al estudiar la gravitación y las leyes de Kepler.

Realizar la siguiente lectura y reflexione acerca de la misma

"Ciencia y tecnología: también son distintas entre sí. La ciencia se ocupa de reunir conocimientos  y organizarlos. La tecnología permite al hombre usar esos conocimientos  para fines prácticos, y proporciona las herramientas que necesitan los científicos en sus investigaciones. Pero la tecnología puede resultar útil o perjudicial. Por ejemplo, contamos con la tecnología para extraer combustibles fósiles del suelo, para después quemarlos y producir energía. La producción de energía ha beneficiado a nuestra sociedad de incontables maneras; por otro lado, pone en peligro al ambiente. Es tentador echar la culpa a la tecnología misma por problemas como la contaminación, el agotamiento de los recursos; sin embargo, estos problemas no son causados por la tecnología, ya que los humanos somos responsables de cómo se usa". HEWITT, PAUL G., Física conceptual, México, Pearson, 1999.

CLIC PARA ACCEDER A PRUEBA DE DIAGNOSTICO. Imprima, desarrolle y presente a su profesor hasta el viernes 27 de septiembre de 2019. valido para un aporte.

UNIDAD 1: INTRODUCCIÓN A LA FÍSICA
LA FÍSICA EN NUESTRO ENTORNO

- Relación de la física con otras ciencias.
- Sistemas físicos
- Sistema internacional de unidades
- Conversión de unidades
- La notación científica
- La teoría de errores
MAGNITUDES VECTORIALES Y ESCALARES
-Vectores.- Definición y ejemplos
-Componentes rectangulares
-Componentes polares
-Componentes geográficas
TRIGONOMETRÍA
-Conceptos trigonométricos
-Funciones trigonométricas
-Resolución de triángulos rectángulos

Ver el vídeo que es la física y áreas de estudio

Sistemas físicos

Un sistema físico es un agregado de objetos o entidades materiales entre cuyas partes existe una conexión o interacción o un modelo matemático de tipo causal (aunque no necesariamente determinista o causal en el sentido de la teoría de la relatividad). Todos los sistemas físicos se caracterizan por:

- Tener una ubicación en el espacio-tiempo.

- Tener un estado físico definido sujeto a evolución temporal.

- Poderle asociar una magnitud física llamada energía.

Sistemas físicos en relación al entorno

Los sistemas físicos pueden ser abiertos, cerrados o aislados, según que realicen o no intercambios con su entorno:

Un sistema abierto es un sistema que recibe flujos (energía y materia) de su entorno, pueden realizar el trabajo de mantener sus propias estructuras e incluso incrementar su contenido de información. El hecho de que los seres vivos sean sistemas estables capaces de mantener su estructura a pesar de los cambios del entorno requiere que sean sistemas abiertos.

Un sistema cerrado sólo intercambia energía con su entorno, en un sistema cerrado el valor de la entropía es máximo compatible con la cantidad de energía que tiene.

Un sistema aislado no tiene ningún intercambio con el entorno.

LA FÍSICA es la ciencia que tiene por objeto el estudio de la materia, la energía, sus propiedades e interacciones. Podemos decir que la Física intenta una explicación del universo, en lo que corresponde tanto al macrocosmos como al microcosmos. Hasta el siglo XVI, la Física no existió como ciencia independiente sino que fue tratada como parte de la Filosofía, con Galileo Galilei, la Física adquiere plenamente su dimensión experimental. 

MAGNITUDES

Para conocer el entorno físico es necesario distinguir las características y propiedades de los objetos o fenómenos naturales  y asignarles un valor. La cualidad que podemos medir de una propiedad física es una magnitud, se clasifican en: fundamentales y derivadas.

LA MEDIDA

Es necesario medir las propiedades de los objetos y fenómenos para detectar las diferencias. La medida es la comparación entre dos cualidades semejantes de dos objetos, para determinar cuántas veces se repite dicha cualidad, cuando uno de ellos se toma como base de comparación (patrón)

SISTEMA INTERNACIONAL DE UNIDADES

Todo patrón de medida se instituye por medio de una convención que las naciones adoptan para efectuar mediciones comunes y evitar confusiones. Los acuerdo sobre la selección y uso de los patrones se establecen en reuniones internacionales de la Conferencia General  de Pesos y Medidas, con sede en París.

En la actualidad se cuenta con un Sistema Internacional de unidades, cuyas siglas oficiales son SI. Este sistema es un conjunto de unidades de medición que se emplea de forma cotidiana en la mayoría de los países del planeta. En el SI existen siete unidades fundamentales, 141 derivadas, que se forman combinando las unidades fundamentales por medio de expresiones algebraicas, dos unidades suplementarias que corresponden a las magnitudes de ángulo plano, de ángulo solido y cuyos nombres son radian  (rad) y estero radian (sr). 

Además del SI, existen otros sistemas de medidas sin embargo son pocos los países que lo emplean. Un ejemplo es el sistema técnico inglés, que se utiliza en Estados Unidos, Australia, Myanmar (antes Birmania) y Liberia entre otros países. Las unidades básicas de este sistema son el pie, ft  (0,3048 m), para la longitud; la libra, lb (0,4535) kg), para la masa; y el segundo para el tiempo. 
CONVERSIÓN DE UNIDADES
Un método muy practico para la conversión de unidades el de factores de conversión. consiste en multiplicar el dato por fracciones que expresan la equivalencia entre la unidad deseada y la unidad del dato. 
Lo que tengo  x   lo que quiero                = lo que quiero
                          Unidad de lo que tengo

Por ejemplo, transformar 72km/h a ft/s (pies/segundo)
72 km  x  1000 m   x  100 cm  x    1ft    __      x     1h _        x   1min_  = 65,62 ft/s
      h       1km           1m            30,48 cm         60 min         60s
1m   = 100 cm
1ft    = 12 pulgadas (in) = 30,48 cm
1 kg = 1000 g
1 tonelada (T) = 1000 kg
1 kg = 2,2 lb
1 lb  = 16 oz (onzas)
1 in (pulgada) = 2,54 cm
1 milla(mi) = 1,609 km
1slug (unidad de masa en el sistema británico) =14,59 kg 
1 lt (litro) = 1dm³ 
Cuadro de magnitudes fundamentales

Las magnitudes derivadas más útiles que se exponen en la siguiente tabla:

Clic para acceder al archivo de trabajo física
La notación científica se utiliza para facilitar la expresión de cantidades muy grandes o muy pequeñas, y los cálculos que se derivan de ellas. Los números se expresan mediante una parte entera de una cifra (diferente de cero), una parte decimal y una potencia de 10 de exponente entero.
Formato de la Notación Científica

La notación científica de un número real es su expresión como el producto de un número mayor o igual que 1 y menor que 10, por una potencia de 10. La forma general de un número escrito a partir de su notación científica es: k x 10ⁿ donde 1 <= k <10 y n ⥺ N
Además, n es negativo cuando corresponde a la expresión de una cantidad muy pequeña y n es positivo cuando se relaciona con una cantidad muy grande.
Aplicando la notación científica a la escritura del diámetro del glóbulo rojo y la distancia de la Tierra al Sol, se obtiene lo siguiente:
0,0065 mm = 6,5 x 10⁻³
Hay tres lugares entre el lugar de la coma y el 6. Por ello, el exponente de la potencia es -3.
150 000 000 000 m = 1,5 x 10¹¹
Hay once lugares entre el final del número y el 1. Por ello, el exponente de la potencia es +11. 
Veamos algunos ejemplos:

Número	¿Notación Científica?	Explicación
1,85 x 10-2	sí	-2 es un entero
1,5 x 101/2	no	no es un entero
0,82 x 1014	no	0.82 no es ≥ 1
10 x 103	no	10 no es < 10

MAGNITUDES VECTORIALES Y ESCALARES 
Vectores.- Definición y ejemplos 

- Reflexión

Cuando alguien nos pide que le alcancemos un kg de azúcar o un litro de leche, no hay problema, lo podemos hacer, pero cuando nos pide que ayudemos a mover un mueble, necesitamos saber cuánta fuerza necesitamos realizar y en qué dirección deberíamos hacerlo. 

En los dos casos hablamos de magnitudes físicas. En el primer caso: el de los kilogramos de azúcar o el litro de leche , se trata de magnitudes escalares, donde para definirlo solo es necesario la cantidad, lo que denominamos módulo. En el segundo caso, el de la fuerza, se trata de una magnitud vectorial, en donde además del modulo necesitamos definir la dirección.

Principales magnitudes
Escalares	Vectoriales
Longitud	Velocidad
Área	Aceleración
Volumen	Fuerza
Rapidez	Corriente eléctrica
Masa	Intensidad de campo gravitacional
Energía	Intensidad de campo eléctrico

para denotar un vector usamos gráficamente la flecha, donde la saeta nos indica la dirección  y la medida de su longitud, el modulo; un vector necesariamente esta emplazado en un sistema de referencia.

En física  llamamos vector a la magnitud que posee modulo, dirección y su unidad correspondiente; en la dirección está incluido el sentido. Además es necesario definir mediante sus coordenadas en un sistema de  referencia ya sea por sus componentes rectangulares, polares, geométricas o por el vector unitario. 

Un vector fijo es un segmento orientado que va del punto A (origen) al punto B (extremo).Los vectores, en física, nos sirven para representar una magnitud física como la velocidad o la fuerza. 

Un vector tiene

- Origen o Punto de Aplicación: es el punto exacto sobre el que actúa el vector.

 - Módulo: es la longitud o tamaño del vector. Para saber el módulo de un vector es necesario conocer el punto inicial y final del vector (origen y extremo). Para calcular el módulo se mide desde el origen hasta el extremo.

- Dirección: viene dada por la orientación en el espacio de la recta que lo contiene. La recta que contiene el vector es su dirección, pero también es el ángulo que tiene el vector con respecto al eje de referencia. Si el eje de referencia es horizontal, el ángulo que forma el vector, con la horizontal, será la dirección.
- Sentido: se indica mediante una punta de flecha situada en el extremo del vector, indicando hacia que lado se dirige el vector.

vídeo, representación de vectores en el plano https://www.youtube.com/watch?v=hUFfjHntdUs
VECTORES EN EL PLANO

• Componentes rectangulares
• Componentes polares
• Componentes geográficas
• Suma de vectores: método del polígono, del paralelogramo y analítico. 

TRIGONOMETRÍA

• Conceptos trigonométricos
• Funciones trigonométricas
• Resolución de triángulos rectángulo

Representación rectangular y polar de vectores en el plano.
Componentes rectangulares.
Todo vector puede ser expresado por sus componentes horizontal y vertical con respecto aun sistema de referencia. Para indicar la dirección de la componente en (x) usamos (i) como unidad del vector, con el signo positivo si va a la derecha y negativo si va a la izquierda; para la componente en (y) usamos (j), con signo positivo si va hacia arriba y negativo si va hacia abajo.
Para denotar un vector usamos una saeta sobre la letra que indica el vector y dado por sus componentes tenemos

Coordenadas polares
Las coordenadas polares indican el modulo y la dirección, dado por la forma, 

siendo A el módulo y q el angulo formado por el vector con respecto al eje de x(+)

Coordenadas geográficas
Las coordenadas geográficas indican el modulo y la dirección expresado en función de los puntos cardinales.
En este caso

ver vídeo aplicación de las funciones trigonométricas 

video de aplicación de funciones trigonométricas

ver vídeo suma de vectores método gráfico (paralelogramo)

Ver vídeo suma de vectores método gráfico (polígono)

Suma de vectores método analítico

Movimiento en una dimensión

Identificar la posición y el desplazamiento de un objeto (considerado puntual) que se mueve, a lo largo de una trayectoria rectilínea, en un sistema de referencia establecida. REF. (CN.F.5.1.1.)

CN.F.5.1.2. Explicar, por medio de la experimentación de un objeto y el análisis de tablas y gráficas, que el movimiento rectilíneo uniforme implica una velocidad constante.

Registrar gráficamente que, en el caso particular de que la trayectoria sea un círculo, la aceleración normal se llama aceleración central centrípeta. REF. (CN.F.5.1.12.)

CN.F.5.1.26. Determinar que el lanzamiento vertical y la caída libre son casos concretos del movimiento unidimensional con aceleración constante (g) mediante ejemplificaciones y utilizar las ecuaciones del movimiento vertical en la solución de problemas.

Describir el movimiento de proyectiles en la superficie de la Tierra, mediante la determinación de las coordenadas horizontal y vertical del objeto para cada instante del vuelo y de las relaciones entre sus magnitudes (velocidad, aceleración, tiempo); determinar el alcance horizontal y la altura máxima alcanzada por un proyectil y su relación con el ángulo de lanzamiento REF. (CN.F.5.1.29.)

3 MOVIMIENTO:
3.1 Posición y desplazamiento.- Posición, trayectoria, distancia y desplazamiento.- definición y gráficas
3.2 Rapidez y velocidad:
3.3 Velocidad media e instantánea.
3.4 Movimiento rectilíneo uniforme
3.5 Aceleración
3.6 Movimiento rectilíneo uniformemente variado. - Movimiento horizontal y Caída libre
3.7 Movimiento de proyectiles.
POSICIÓN Y DESPLAZAMIENTO
Es importante señalar la diferencia que hay entre espacio recorrido y desplazamiento ya que son, en general, conceptos distintos que se suelen confundir. El espacio o distancia recorrido es una magnitud escalar que se mide sobre la trayectoria. El desplazamiento es una magnitud vectorial que sólo depende de la posición inicial y final del cuerpo y es independiente de la trayectoria 

Trayectoria.- corresponde al camino seguido por una partícula o un cuerpo que se desplaza. 

Posición.- Es un punto en el espacio respecto a un sistema de referencia. representa el vector que une el lugar ocupado por el cuerpo con el origen del sistema de referencia 
La ecuación de posición o ecuación de trayectoria representa el vector de posición en función del tiempo. Su expresión, en coordenadas cartesianas y en dos dimensiones viene dada por:

La rapidez es una magnitud escalar que relaciona la distancia recorrida con el tiempo, representa el modulo de la velocidad. 

La velocidad es una magnitud vectorial que relaciona el cambio de posición (o desplazamiento) con el tiempo.
En el Sistema Internacional, la unidad para la rapidez media es el m/s (metro por segundo). 

clic para acceder al vídeo: Cinemática, velocidad, desplazamiento, distancia, gráficas
MOVIMIENTO RECTILÍNEO UNIFORME
Cuando un cuerpo mantiene su velocidad constante, es decir, recorre distancias iguales en tiempos iguales, decimos que su movimiento es rectilíneo uniforme, sintetizado en las siglas MRU.

Velocidad constante implica rapidez constante y movimiento rectilíneo, ya que al tener velocidad constante su dirección también sera constante y por tanto su movimiento sera rectilíneo.
En el movimiento rectilíneo la velocidad instantánea es igual a su velocidad media.
es decir:
                      V= ∆r/t
y su rapidez
                       V= d/t
Ejemplo. el auto tiene una velocidad constante V=10 m/s lo que quiere decir que cada segundo recorre 10 m.
Ecuaciones y gráficas
Posición.- Su unidad en el Sistema Internacional (S.I.) es el metro (m) y se obtiene por medio de la siguiente expresión:

Donde:

     xo es la posición inicial.
     v es la velocidad que tiene el cuerpo a lo largo del movimiento.
     t es el intervalo de tiempo durante el cual se mueve el cuerpo.

En aquellos casos en los que la posición inicial es cero ( x0 = 0 ), la distancia recorrida y la posición coinciden, y su valor es:

d=v⋅t

Un bus avanza con MRU a 72 km/h. determinar el tiempo que tarda en avanzar 200 m

ver solución

Mario y Luis se mueven con MRU y van al encuentro. Calcular el tiempo que emplean para encontrarse; sabiendo que Mario va a 10 m/s y Luis a 5 m/s, y la distancia de separación es de 300 m.

ver solución  
1. Pedro va al colegio caminando desde su casa. La distancia que debe recorrer es de 410 m. Si tarda 6 min 24 s en llegar, ¿cuál es la velocidad de Pedro?

2. Un ciclista se encuentra en el kilómetro 25 de una etapa de 115 km. ¿Cuánto tiempo tardará en llegar a la meta si rueda a una velocidad de 60 km/h?

3. Si los animales tuvieran sus propios juegos olímpicos, según estos datos, ¿cuál obtendría la medalla de oro en una carrera de 200 metros lisos?

    Oso perezoso 0,2 km/h
    Caraco l 50 m/h
    Tortuga 70 m/h 

4. Un ave vuela a una velocidad constante de 15 m/s. a. Confecciona una tabla que recoja las posiciones del ave cada 5 s durante un vuelo de 30 s.  b. Dibuja en tu cuaderno la gráfica posición tiempo del ave a partir de los valores registrados en la tabla.